 Espero, querido lector, que el título no le haya asustado, aunque en la actual situación en que nos encontramos, tiene un aire agorero acongojante. Pero no, no va de eso. Me da un poco de vergüenza confesarlo, pero este post trata de algo muy importante, que debí haber escrito en enero (hablé del fin del mundo, que la verdad tampoco es moco de pavo), y que sólo ahora he recordado, al ver un artículo titulado "Chaos at fifty" ("El caos a los cincuenta"), de Adilson E. Motter y David K. Campbell. Y el caso es que el pasado enero se cumplieron 50 años de la publicación de un artículo titulado "Deterministic nonperiodic flow" ("Flujo determinista no periódico"), de Edward Norton Lorenz (1917-2008), que aparece en la foto estudiando sus simulaciones numéricas.
Espero, querido lector, que el título no le haya asustado, aunque en la actual situación en que nos encontramos, tiene un aire agorero acongojante. Pero no, no va de eso. Me da un poco de vergüenza confesarlo, pero este post trata de algo muy importante, que debí haber escrito en enero (hablé del fin del mundo, que la verdad tampoco es moco de pavo), y que sólo ahora he recordado, al ver un artículo titulado "Chaos at fifty" ("El caos a los cincuenta"), de Adilson E. Motter y David K. Campbell. Y el caso es que el pasado enero se cumplieron 50 años de la publicación de un artículo titulado "Deterministic nonperiodic flow" ("Flujo determinista no periódico"), de Edward Norton Lorenz (1917-2008), que aparece en la foto estudiando sus simulaciones numéricas.
Tras ese inocente título se esconde uno de los mayores cambios de paradigma de la física, de la ciencia, y de nuestra manera de ver el mundo. Efectivamente, hasta esa época se creía que los sistemas dinámicos (aquellos que evolucionan en el tiempo) sólo podían tener tres tipos de comportamientos: tender a un estado estacionario (también llamado punto fijo) en el que dejan de modificarse; variar periódicamente, recuperando su comportamiento en un instante dado al cabo de un cierto período fijo y constante, o el llamado movimiento cuasiperiódico, que es la combinación de movimientos periódicos con períodos cuya relación no es un número racional, por lo que el sistema vuelve a ser casi como era cada cierto tiempo pero nunca exactamente. La verdad es que si uno lo piensa ingenuamente, no parece que vaya a haber otros tipos de evolución temporal, ¿no? ¿Cómo serían esos tipos adicionales?
Eso es lo que hace Lorenz en su trabajo: mostrarnos que hay un cuarto tipo de movimiento, que el llamó "no periódico" y que nosotros llamamos hoy "caótico". Lorenz era un meteorólogo (y de hecho el artículo está publicado en Journal of Atmospheric Sciences) que estudiaba el flujo de convección en un fluido situado entre dos capas fijas a temperaturas distintas (convección de Rayleigh) como modelo de uno de los mecanismos básicos de la circulación atmosférica. Simplificando matemáticamente las ecuaciones de dicho fenómeno, obtuvo las hoy famosas ecuaciones de Lorenz:
Para esta discusión, no nos importa mucho qué representan las variables X, Y y Z, aparte de que describen la ya citada convección de manera muy estilizada. Como Lorenz no sabía resolverlas (ni nadie hasta hoy en día) lo que hizo fue integrarlas numéricamente con uno de los primeros ordenadores, y lo que vio fue esto:
Lo que representa esta gráfica es la evolución temporal de la variable Y durante tres mil pasos temporales (mil en cada línea). Como vemos, estamos ante un tipo de evolución que sorprendió a Lorenz porque no encajaba en ninguna de las clasificaciones que conocía. Con los ordenadores de hoy en día, uno puede repetir este trabajo durante los pasos que quiera, y nunca encontrará que se repita algún patrón. Bienvenidos al mundo del caos (nombre que acuñaría unos años más tarde uno de los grandes pioneros de esta línea de investigación, Jim Yorke).
Con todo, lo importante no es que el movimiento no sea ni siquiera cuasiperiódico. Lorenz se dio cuenta de que pasaba algo muy extraño, y así lo escribió en el abstract del artículo: "(...) se encuentra que las soluciones no periódicas son normalmente inestables bajo pequeñas modificaciones, de manera que estados iniciales ligeramente distintos pueden evolucionar hasta convertirse en considerablemente diferentes." Esto es lo que técnicamente llamamos "dependencia exponencial de las condiciones iniciales" y popularmente ha acabado siendo conocido como "el efecto mariposa" (debido a una conferencia que, cuando su trabajo empezó a ser reconocido tras años de dormir en los estantes de las bibliotecas, el propio Lorenz pronunció en 1972 ante la AAAS bajo el título "Does the flap of a butterfly's wings in Brazil set off a tornado in Texas?" ("¿Origina el aleteo de una mariposa en Brasil un tornado en Texas?"). Aquí he de decir, antes de que alguien me corrija en los comentarios, que ya Poincaré había anticipado este fenómeno en 1909, sin llegar a dar ejemplos como el que ahora presentaba Lorenz.
Para ilustrar esto, voy a utilizar un sistema más sencillo que el de Lorenz: la ecuación logística o de Verhulst, un modelo extraordinariamente sencillo del crecimiento de una población limitada por la necesidad de un recurso. En 1976, el biólogo teórico Robert May (hoy Lord May of Oxford) publicó un artículo, también muy apropiadamente titulado "Simple mathematical models with very complicated dynamics" ("Modelos matemáticos sencillos con dinámicas muy complicadas") en el que mostraba que esta aparentemente sencilla recursión
también daba lugar a secuencias de números x que no se repetían ni caían en ciclos (salvo para algunas excepciones en las que el primer número de la recursión se elige expresamente), es decir, al equivalente discreto del movimiento caótico. Y, como tal, exhibe también esa dependencia de las condiciones iniciales, cómo pone de manifiesto el siguiente ejemplo:
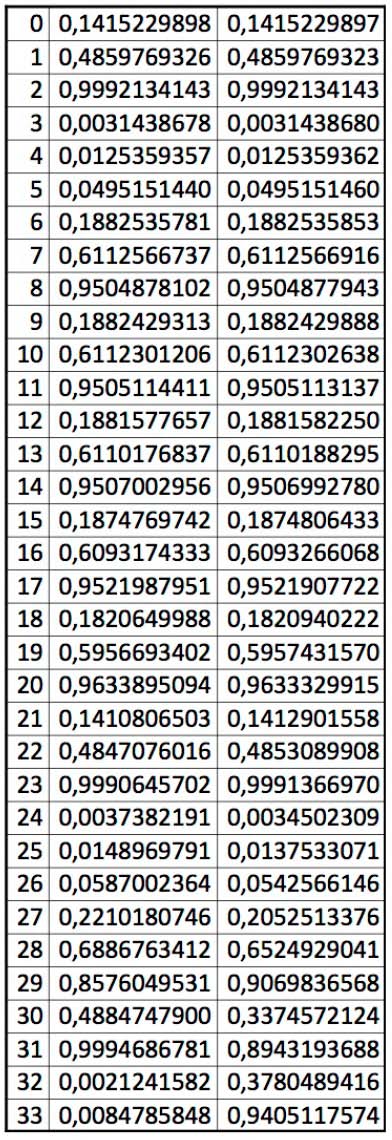
En la tabla se recogen dos recursiones generadas a partir de la ecuación de arriba, partiendo de los valores que se indican para t=0 (t, o el número de iteración, se recoge en la primera columna), y que se diferencian sólo en la décima cifra decimal. Así, vemos que en la iteración 14, la diferencia está ya en la quinta cifra decimal, y en la iteración 29, ¡todas las cifras son distintas! Para que esto no quede en números, le dejo también una muestra de las gráficas que estudiaba tan atentamente Lorenz:
Aquí, en esta "inestabilidad", que decía Lorenz, radica el gran cambio de paradigma que supuso la teoría del caos. Recordemos que hasta este momento, la idea dominante en la física era la del "universo mecánico" ("clockwork universe"), que había sintetizado Laplace cuando en 1820 escribió aquello de que "(...)si este intelecto fuera lo suficientemente vasto como para someter los datos a análisis, podría condensar en una simple fórmula el movimiento de los grandes cuerpos del universo y del átomo más ligero; para tal intelecto nada podría ser incierto y el futuro así como el pasado estarían frente sus ojos." (De nuevo, antes de que me corrijan en los comentarios, este determinismo se había roto ya con la aparición a principios del siglo XX de la mecánica cuántica, pero todo el mundo daba por hecho que la indeterminación cuántica se limitaba al mundo submicroscópico y que no tenía ningún impacto en nuestra vida cotidiana). Pero claro, nosotros no somos ese intelecto perfecto del que habla Laplace, y conocemos el estado actual del universo con cierto margen de error, que proviene de nuestra ineptitud, o de nuestros aparatos de medida. Volviendo al ejemplo anterior, si nos hemos equivocado en la décima cifra decimal de nuestro dato inicial, al cabo de tan sólo 33 iteraciones no somos capaces ni siquiera de decir si nuestro sistema va a estar a la izquierda o la derecha de 1/2. Fíjese, querido lector, que ya no hablo de intentar predecir el número exacto, sino simplemente ¡si está a un lado o a otro! Lo haríamos igual de bien echándolo a cara o cruz...
Es muy importante que observemos que en esto del caos no hay nada aleatorio. Absolutamente nada. Las ecuaciones son puramente deterministas, y si siempre les metemos el mismo dato, producen el mismo resultado como respuesta. Es más, ni siquiera estoy diciendo que sea imposible predecir: a corto plazo, las trayectorias del sistema no se ven muy afectadas por el error inicial. Si en el ejemplo, para mis propósitos, me bastase tener cinco cifras correctas, puedo predecir bien 13 pasos temporales. Ningún problema; no hay nada mágico en la ley de la evolución. Lo que está pasando es que como el dato inicial no se conoce con precisión infinita, sólo podremos saber qué le va a pasar al sistema durante una cierta ventana temporal, ventana que aumentará cuanto mejor conozcamos el punto de partida, claro, pero que nunca será infinita.
¿Le suena esto de algo? Sí, seguro que sí, y a Lorenz también: a las predicciones meteorológicas, que era lo que él estudiaba. Traduzco de las conclusiones de su artículo: "Cuando nuestros resultados sobre la inestabilidad del flujo no periódico se aplican a la atmósfera, que es ostensiblemente no periódica, indican que la predicción de un futuro suficientemente lejano es imposible por ningún método, a no ser que las condiciones actuales se conozcan exactamente." Así de claro. Aunque uno conozca perfectamente las leyes físicas que rigen la dinámica atmosférica, nunca, nunca, nunca podrá predecir el tiempo (que no el clima, aviso para negacionistas del cambio climático, que no es la misma cosa) más allá de un cierto intervalo. Intervalo que hoy en día, después de elaborar modelos muy completos y mejorar la precisión con la que medimos las condiciones atmosféricas, llega a dos o tres días.
La cosa está, querido lector, en que este paradigma de la impredecibilidad determinista es muy general. El caos aparece en la mayoría de los sistemas físicos, ya que lo que se necesita para su aparición es muy poco: que el sistema sea no lineal: es decir, que la evolución de las magnitudes de interés no sea simplemente proporcional a ellas mismas, sino que tenga términos cruzados, o potencias, como los términos XY y XZ en las ecuaciones de Lorenz o el x cuadrado de la ecuación logística. Esto, para bien o para mal, es la regla, no la excepción. De aquí la importancia del descubrimiento de Lorenz. No hablamos sólo de predecir el tiempo, sino de predecir en general. Y eso afecta también a la evolución de la economía, claro, que se rige habitualmente por ecuaciones no lineales; pero de la historia del caos en la economía, de lo que puede aportar y ha aportado hasta ahora, hablará Jesús Fernández Villaverde (mucho más autorizado que yo para ello, dónde va a parar) en un post que aparecerá el próximo 23 de julio. Cuánto vayamos a poder predecir de las magnitudes que nos interesan dependerá de las ecuaciones que las rijan y de lo bien que sepamos cómo estamos ahora. En todo caso, a partir del trabajo de Lorenz, siempre tendremos que tener presente que nunca podremos predecir la economía, o el tiempo, o la trayectoria de la Tierra, o lo que sea, en un futuro arbitrariamente lejano. Je suis désolé, monsieur Laplace, c'est la vie.




Hay 34 comentarios
Interesante.
Para volver a algo menos alejado de la España economico y social de hoy, que es el tema principal de Nada es Gratis (a parte de las ilustraciones de Anxo para meros mortales):
d(corrupcion)/dt= k (corrupcion), k>1
Eso implica un crecimiento exponencial de la corrupción, que físicamente es imposible dado que la población es finita. Tendría que ser una ecuación logística como la del post...
Hola,
Interesante artículo, Anxo. En cuanto a esto último creo que estás equivocado. En realidad, si la derivada de la variable corrupción es una constante (k), el crecimiento de la variable corrupción con respecto del tiempo es lineal con pendiente k>1
Muchas gracias!
Una exposición muy pedagógica. De hecho, para hacer las cosas aún mas complejas, tambien hay procesos estocásticos caóticos (por ejemplo Wiener Caos, see: Norbert Wiener American Journal of Mathematics, 60, 4, 897-936).
Lo cierto es que aunque los sitemas caóticos sean deterministas, pueden definirse medidas en el espacio de estados como límite the las frecuencias relativas con que se visitan. En el fondo no importa tanto si la realidad es determinista o estocástica, ambos enfoques pueden estudiarse con medidas de probabilidad. Los estadísticos realizan simulaciones usando generadores de números pseudo-aleatorios deterministas porque en realidad, no importa distincion. El concepto de ser "determinista" o ser "estocástico" es una percepción humana, una sensación dada por la (im)posibilidad de prever futuros outcomes de un sistema cuando se dispone de información previa del pasado del sistema.
Anxo, no nos das ninguna oportunidad. Con lo que hubiéramos presumido de apuntar que Poincaré ya lo había dicho.
Más en serio, me he pasado años discutiendo esa idea tan arraigada de que la economía no es una ciencia "dura" como la física porque al fin y al cabo detrás de la economía hay personas, seres humanos, que son impredecibles.
Puede que la impredictibilidad sea un elemento esencial, pero no sólo las personas son impredecibles. Siempre me ha parecido que la ciencia hermana de la economía es la metereología. En ambos casos partimos del caos micro -- en un caso consumidores y empresas, en el otro partículas en la atmósfera -- y esperamos que al menos en el agregado surja alguna regularidad a la que aferrarse. En ambos casos, también, nuestra capacidad de predicción es más bien limitada: unos días en el caso de la metereología y quizás unos meses en el caso de la economía, y eso con intervalos de confianza king size.
Gracias Jorge. Poincaré era muy grande. Si hubiera vivido en la era de los ordenadores, hubiera sido la bomba. Sólo puedo imaginarme su frustración...
En cuanto a tu segundo comentario, estoy muy de acuerdo. Tendría que haber una "economía mecano-estadística" que nos llevara de la micro (mecánica clásica o cuántica en física) a la macro (termodinámica en física). Pero parece muy difícil, y creo que el problema radica en que la interacción entre personas, al ser estratégica, es mucho más complicada de abordar.
Este artículo de Duncan Foley va un poco de eso. Lo tengo en la mesa desde hace años pero nunca he conseguido leerlo.
Sí parece ir de eso, sí. Si tienes el pdf te agradecería que me lo enviaras.
PS. En realidad, encontrar un buen generador de números pseudo aleatorios no es fácil. de conseguir. Por ejemplo, el sistema dinámico
X(t+1)=(a X(t)+c) mod m
(con modulo m>0, multiplicador 0<a<m, e incremento 0<=c<m donde c y me son primos relativos) se utiliza en el llamado "Linear Congruential Generator".
Si se usan parámeros irracionales la secuencia es caótica, pero con números racionales se obtiene una secuencia periodica con periodo m.
En la práctica, las simulaciones se basan en números racionales, y se obtienen secuencias periódicas. Las mejores simulaciones requieren parámetros tales que se generan soluciones con periodos muy largos, en tal caso al coger solo una parte de la secuencia se parece mucho a una solución caótica y puede ser manejada como si fuera estocástica. Pero con otros valores no se parece nada, para comprobar esta idea basta jugar en este simulador
http://demonstrations.wolfram.com/LinearCongruentialGenerators/
Muy buen artículo Anxo. Simplemente querría matizar un poco tu conclusión final, porque no es tan drástica como la has pintado. Lo que realmente hace el caos es generar espontáneamente azar en modelos deterministas. No es que el modelo no sea determinista (lo es, como bien hasa aclarado), sino que las predicciones ya no lo pueden serlo. La manera de predecir con ecuaciones caóticas es estudiar cómo se transforman intervalos enteros, no condiciones iniciales aisladas. Eso lleva a que al final uno acaba teniendo una distribución de probabilidad que le dice cuál es la probabilidad de que, en un instante dado, su trayectoria esté en un cierto intervalo (en el mapa de Lorenz podría ser cuál es la probabilidad de que la trayectoria quede por encima o por debajo de 1/2). Las ecuaciones resultantes para la evolución de esas distribuciones de probabilidad son también deterministas, pero a diferencia de las trayectorias, las distribuciones de probabilidad son perfectamente predecibles. Y es por este motivo que ahora vemos la predicción del tiempo como "probabilidad de lluvia 70%". Es decir, no podemos predecir trayectorias, pero sí distribuciones de probabildad, cuyo comportamiento asintótico puede ser muy estable (las del mapa logístico o el de Lorenz lo son, como bien sabes). Por eso se trata de un gran cambio de paradigma, en mi opinión (y por razones parecidas) comparable al de la mecánica cuántica.
(No sé si al final la aclaración ha oscurecido más bien.)
Gracias Jose, muy buena puntualización. Algo tenía que dejar para que se pudiera aportar en los comentarios! Creo que lo has explicado muy bien y el paralelismo que apuntas con la mecánica cuántica en términos de distribuciones de probabilidad es muy interesante.
Vaya, se me ha adelantado Jose M Vidal. No había visto su comentario, que apunta lo mismo que el mío. Y me gusta mucho su apunte de que determinismo y estocasticidad están ligadas a la percepción humana.
¡Me alegro de pertenecer a la "generación del caos"!
Agradezco también el escrito, y agradecería aún más que disipáseis un poco mi ignorancia: ¿Hay relación entre el "caos" de Lorentz - Poincaré y la "incertidumbre" de Keynes?
Pues ahí me has pillado... A ver si algún economista de los que nos leen te puede ayudar...
No mucha. Keynes intento formular, sin demasiado exito (como el mismo reconocio) una teoria de la probabilidad basada en creencias subjetivas sobre probabilidades y que implicaba que estas podian cambiar relativamente rapido y por tanto generar fluctuaciones en la demanda agregada. Despues de muchos años de lucha (que Skideslky refleja muy bien en su biografia) y de muchas desilusiones, dejo de trabajar en el area y su discusion del tema en la Teoria General es heuristica.
Una buena lectura es "An attempt at reading Keynes' Treatise on Probability" de Christian P. Robert (http://arxiv.org/abs/1003.5544). Robert es quizas uno de los estadisticos mas importantes hoy en el mundo.
Gracias Jesús, es un interesante problema, sólo que difícil (como todo lo interesante por otra parte).
Jesús, aprovechando que el Pisuerga.... Nos hablado en muchas ocasiones de la revolución de los Big Data. Acaba de publicarse la traducción de un libro de Viktor Mayer-Schönberger y Kenneth Cukier justamente con ese título. ¿Lo conoces? ¿Merece la pena?
Muchas gracias!
Excelente artículo. Y espero el que anuncias del Prof. Fernández Villaverde. Intuyo que quizás en él hable de la consecuencia lógica historicamente del caos, los fractales; y si ha habido o no influencia de los trabajos de Mandelbrot en economía.
Aprovecho para peguntar si otros nuevos paradigmas que a veces se oyen referidos a la transferencia desde las ciencias "duras", matemáticas y física fundamentalmente, a la economía son o no importantes como tales cambios de paradigmas o si solo son nuevas herramientas que resuelven casos puntuales. Me refiero a áreas como la econofísica, las redes neuronales, la lógica difusa, etc..
Saludos.
Gracias Juanjo. Responder a tu pregunta exigiría casi un post nuevo por cada punto de los que citas. Por decir algo breve, mi impresión personal es que ni aportan tanto como dicen sus promotores, ni se puede despreciar alegremente su aportación como hace mucha gente "ortodoxa". Luego ya habría que discutir caso por caso.
Como conclusión preliminar antes del día 23 y para ver si lo he entendido: ¿esto quiere decir que a las predicciones de Niño Becerra, ni caso? 😉
Anxo eres un crack!
Como siempre laro y pedagógico
Un abrazo, Pablo
Gracias Pablo!
El origen del celebre "efecto mariposa" como lo describe el propio Lorenz en un libro publicado por Ed Debate (La Esencia del Caos,1995) tuvo un origen "0scuro".Al parecer iba a dar en el año 1972 una conferencia en el congreso de la AAAS en Washington DC en la que el ejemplo que el solía utilizar era el aleteo de una gaviota. Sin embargo el presidente de la sesión -Philip Meriles- no pudo contrastar el titulo de la conferencia y puso mariposa en vez de gaviota. La conferencia se titulaba "Predecibilidad. El aleteo de una mariposa en Brasil ¿originó un tornado en Texas?". Entonces no se publico. Solo años más tarde la incluyo como Apéndice I en el libro que cito (versión inglesa The Essence of Chaos, University of Washington Press 1993).Es un magnifico libro e ideal para los que no estamos versados en ciencia dura (matemáticas o física) como sucede por otra parte con sus artículos. Enhorabuena y adelante.
Muchas gracias rafaestella. Interesante historia y buena referencia. Otro libro muy conocido y creo que bueno de divulgación sobre el caos es "Chaos", de James Gleick (hay una traducción reciente).
Bueno, la traducción no es tan reciente. Es del año 1994, cuando la publicó Seix Barral. Creo que, además, es bastante mala, el primer párrafo es terrible. La de Crítica es una mera reimpresión.
Gracias por los datos. Yo lo leí en inglés así que no puedo juzgar.
Para los legos en la materia como un servidor, os recomiendo el libro La mariposa y el tornado. Teoría del Caos y Cambio Climático, RBA, Barcelona, 2011 (ISBN 978-84-473-7435-9) de Carlos Madrid. Advierto que es el único libro que conozco y he leído sobre el tema. No obstante, comenta todo lo que has dicho con más detalle.
"documental matemático sobre sistemas dinámicos, el efecto mariposa y la teoría del caos para todos los públicos" .
http://divulgamat2.ehu.es/divulgamat15/index.php?option=com_content&view=article&id=14700&directory=67
http://www.chaos-math.org/es
Los comentarios están cerrados.