Por Miguel Casares (Universidad Pública de Navarra)
 Hace unos días se puso en circulación el documento de trabajo “A Dynamic Model of COVID-19: Contagion and Implications of Isolation Enforcement” escrito por el profesor Hashmat Khan y por Miguel Casares (yo mismo). Nuestro modelo se basa en la metodología tradicional SIR, que surge del artículo seminal de Kermack y McKendrick publicado en 1927, y que se utiliza habitualmente para estudiar la evolución de las epidemias. El modelo determina la probabilidad diaria, , de que una persona no infectada se contagie de COVID-19 calculando el siguiente producto
Hace unos días se puso en circulación el documento de trabajo “A Dynamic Model of COVID-19: Contagion and Implications of Isolation Enforcement” escrito por el profesor Hashmat Khan y por Miguel Casares (yo mismo). Nuestro modelo se basa en la metodología tradicional SIR, que surge del artículo seminal de Kermack y McKendrick publicado en 1927, y que se utiliza habitualmente para estudiar la evolución de las epidemias. El modelo determina la probabilidad diaria, , de que una persona no infectada se contagie de COVID-19 calculando el siguiente producto
donde A es la probabilidad de contagio en cada contacto diario que dependerá de muchos factores como la protección que llevemos, la duración del contacto, la proximidad de zonas de transmisión (manos, boca, etc.) o la carga viral que lleve el infectado. B es el número de contactos interpersonales que tenemos cada día por trabajo, ocio, compras, etc. C es el ratio entre el número de infectados y la población, que determina la probabilidad de que cualquier contacto que tengamos sea con una persona infectada. Este ratio va creciendo conforme avanza la pandemia. Si Z es el número de personas no contagiadas (susceptibles de contagio) en un día dado, el número total de contagios nuevos en ese día será
Ambos estadísticos varían a medida que avanza la pandemia. Al principio, el número total de contagios aumenta porque aumenta la probabilidad de cruzarse con alguien infectado (aumenta C) y, después, naturalmente, el número de contagios cae (en el extremo, si toda la población estuviera ya infectada, trivialmente no habría nuevos contagios). Es decir, con el paso del tiempo, va quedando menos gente sin contagiarse y C aumenta muy poco mientras que Z va cayendo. Al final, en algún momento, se alcanza un valor máximo fijo del número acumulado de infectados totales. Respecto al número de personas que están infectados cada día, hay que ir restando la gente que se cura o que fallece. En nuestro trabajo suponemos que después de un número fijo (T) de días los infectados se recuperan o mueren con cierta probabilidad exógenamente dada. Cada día t salen de la lista de infectados la gente que se contagió el día t-T. La evolución del número de infectados que todavía tienen el virus tiene forma de una campana con dos fases (ver líneas discontinuas de la Figura 1). Fase alcista: la serie crece lentamente al principio, se va acelerando y a partir de un punto de inflexión se desacelera hasta alcanzar el máximo. Fase bajista: la serie cae despacio al principio, en seguida se acelera el decrecimiento pero a partir de un punto de inflexión la fase bajista es más lenta.

Un menor número de contactos diarios (aislamiento) afecta a la campana de la serie diaria de personas infectadas todavía con el virus de las siguientes 3 maneras (ver, de nuevo, Figura 1):
• Disminuye el máximo (campana desplazadas hacia abajo)
• Aumenta el periodo que va desde el inicio de la pandemia al final de la pandemia (aumenta la base de la campana)
• Se retrasa la epidemia (campana desplazada hacia la derecha)
En nuestro artículo usamos los datos de España: Una población total de 47 millones. La probabilidad de contagio cuando se produce un encuentro con un afectado (A) la fijamos en 1,1% para replicar el periodo medio de días que se necesitan para doblar el dato (doubling time) de número de muertos en la serie observada en España durante las últimas semanas. El dato de doubling time inicial era de 2 días aunque afortunadamente ha aumentado a 4 días con las últimas observaciones. Suponemos que el número de contactos interpersonales diarios, B, es 25 para representar el grado de interacción social y económica que se observa en España (aún siendo conscientes de la heterogeneidad presente en este comportamiento). Siguiendo los estudios epidemiológicos de Anderson et al. (2020) fijamos como tiempo de incubación 6 días, la duración promedio de la enfermedad (incluyendo la incubación) son 20 días y la probabilidad de fallecimiento tras el contagio de COVID-19 es 0,75% (considerando el número estimado de infectados reales que incluye aquellos que no desarrollan síntomas o no se les hace el test por tener sintomatología leve). Por último, Ferguson et al. (2020), basándose en un trabajo realizado por investigadores del Imperial College London, estiman, adaptando datos de China a la realidad social y demográfica de Gran Bretaña, que la probabilidad de que la infección requiera ingreso hospitalario es el 4.4% sobre el total de infectados. Nosotros decidimos aumentar este porcentaje en un 20% para reflejar el hecho de que la población española tiene un envejecimiento más acusado que la de China o Gran Bretaña, y que la enfermedad tiene incidencia principalmente en este tramo de edad. Por ese motivo, hemos considerado que la tasa de hospitalización para infectados en España es el 5,28%. Si bien esta tasa puede aparentar ser baja, cabe recordar que nuestra variable de número infectados incluye a las personas asintómaticas y a aquellas a las que desarrollan síntomas pero no se les hace el test.
Una vez calibrado el modelo simulamos los efectos que la imposición del aislamiento domiciliario que conlleva el Estado de Alarma en España tiene sobre la evolución de la epidemia y sus implicaciones sobre las necesidades de atención hospitalaria. El Estado de Alarma declarado el 14 de marzo se incorpora al modelo como una reducción en el número medio de contactos interpersonales diarios desde 25 hasta 3. El endurecimiento del confinamiento por la suspensión de toda actividad productiva no básica (29 de marzo) se incorpora asumiendo que los contactos interpersonales se van a reducir un 40% adicional. Las líneas rojas de la Figura 2 recogen la evolución del número de contagios, las muertes acumuladas y las necesidades de hospitalización de personas antes y después de la proclamación del Estado de Alarma (identificado por la línea punteada vertical sobe el día 61 en los gráficos).
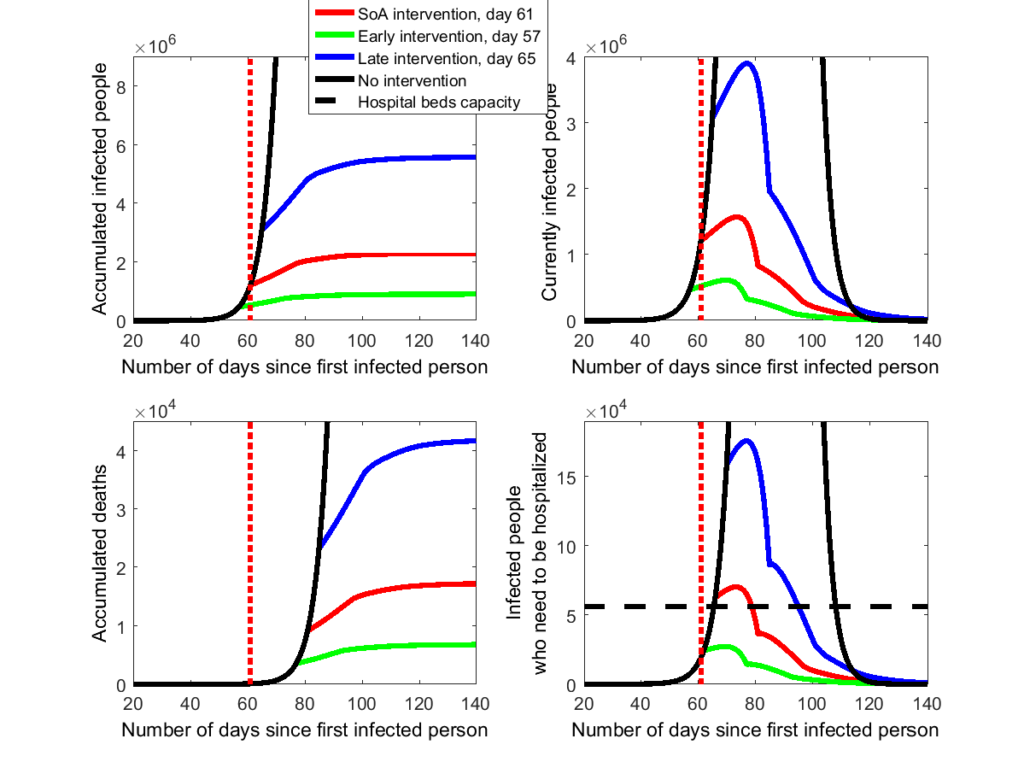
Los resultados más sobresalientes que encontramos son los siguientes:
1. Dados los supuestos del modelo, si no se hubiera tomado ninguna medida de aislamiento social, los contactos entre infectados y no infectados condenarían a casi toda la población a infectarse y más de 350.000 españoles morirían.
2. Estimamos que el Estado de Alarma reduce el número de muertes acumuladas al final de la pandemia en un 95% (quedando la estimación en unos 17.000 fallecidos) y el número diario máximo de camas de hospital necesarias en un 92%.
3. Si el Estado de Alarma se hubiera declarado con anterioridad o se caracterizara por una acción de distanciamiento social más estricta, las reducciones de infectados, fallecidos y hospitalizados habrían sido significativamente mayores. Por ejemplo, si se hubiera anticipado sólo 4 días el número de contagios totales podría haberse disminuido en un 60%.
4. Nuestro modelo predice que los máximos en el número de hospitalizaciones por coronavirus se observarán entre el 27 de marzo y el 4 de abril.
5. Para acercarnos a cifras bajas en el número de contagios se va a necesitar bastante tiempo. Aunque al principio los descensos en el número de nuevos contagios serán importantes, después de una o dos semanas se ralentizará la caída. El 14 de mayo (2 meses después de la declaración del Estado de Alarma) la predicción indica que el número de casos que requieren hospitalización será de 1630 personas (el 2.3% del máximo valor obtenido en la serie diaria). Si esta estimación se cumpliera, las autoridades sanitarias deberían mantener el aislamiento domiciliario y las restricciones a la movilidad (quizás, con alguna medida de flexibilización) para evitar un repunte del número de contagiados por un tiempo mayor que el inicialmente previsto en el Estado de Alarma.
Nuestro trabajo se ha basado en un modelo de agente representativo muy sencillo. Además de la posibilidad de calibrarlo para otro país (Corea del Sur es un caso paradigmático que debería de compararse a los de España o Italia), pueden plantearse varias extensiones al modelo que incorporen agentes heterogéneos. Quizás la más interesante sería la diferenciación de los individuos por edad, dada la distribución desigual tanto de los fallecimientos como los contagios que requieren hospitalización (muy concentrados en personas mayores de 70 años). También podría distinguirse entre contagios que resultan asintomáticos y aquellos que desarrollan los síntomas leves (y que habitualmente no efectúan el test). Para poder hacer estas predicciones sería deseable tener el desglose de infectados por edades. Por último, seguramente un aspecto muy relevante, pero que complicaría el modelo sustancial, es la distribución espacial de los contagios dado que la aparición de focos de contagio iniciales determina claramente la evolución de la epidemia. Creemos que esto es importante porque parece razonable suponer que la densidad de población afecta a la capacidad de infección del virus ya que hay muchas más interacciones entre 1000 madrileños que 1000 habitantes de Zamora, por ejemplo. Esto también ayudaría a hacer una mejor previsión de la capacidad hospitalaria para soportar la evolución de la pandemia.
Cualquier esfuerzo serio de investigación sobre el COVID-19 puede generar una retribución tremenda para la sociedad. Además de evaluar los efectos económicos que (algunos macroeconomistas ya lo están haciendo), una previsión adecuada de la evolución de los contagios y de los efectos que tienen la políticas de contención sobre dicha evolución es clave para minimizar el inasumible coste de pérdidas humanas y evitar el colapso sanitario. Queda mucho trabajo por hacer y, aunque parece factible que se pueda desarrollar una vacuna contra el COVID-19 en los próximos meses, siempre nos quedará la amenaza de una nueva pandemia global con la aparición de un nuevo virus.


Hay 13 comentarios
Un gran y laborioso estudio. Esperemos que al menos se cumplan las previsiones y no se amplíen los fallecidos
Gracias por tu post, Miguel, que tiene un valor didáctico importante. Lo que no creo que tenga es mucho valor predictivo, porque es demasiado sencillo. Como contaba en mi post del lunes https://nadaesgratis.es/admin/lecciones-del-covid-19-sobre-ciencia-que-no-aprenderemos, hay muchos modelos; allí mencionaba alguno que ya incorporaba movilidad y espacio más explícitamente (los de Arenas y Gómez Gardeñes y de Moro y Moreno) y otros ya mucho más pegados a la realidad (Vespignani, Colizza; estos últimos se han usado para predecir picos de gripe estacional con dos semanas de adelanto con bastante éxito). Eso por no hablar del famoso estudio del Imperial College que dice que tenemos ya 7 millones de infectados del que tanto se habla últimamente. Incluir todas estas cosas cambia mucho todas las predicciones (en un sentido o en otro) y sobre todo permite estudiar las políticas en más detalle tocando cosas que en el modelo del que hablas no presenta. En un comentario a mi post, Juan mencionaba este artículo reciente de Science https://www.sciencemag.org/news/2020/03/mathematics-life-and-death-how-disease-models-shape-national-shutdowns-and-other dónde se discuten todas estas cosas. En resumen, no creo que debamos tomarnos al pie de la letra las conclusiones del post (ni, por supuesto de ninguno de los centenares de modelos sencillos que están apareciendo estos días, al menos como preprints). Por eso es tan difícil para las administraciones tomar las decisiones que se están tomando ahora, tienen que trabajar con mucha incertidumbre.
Hola, Anxo, gracias por tu comentario. Tienes razón en que el modelo es demasiado sencillo para explicar la realidad: es de agente representativo y no incluye diferenciación ni espacial (relevante para detectar focos de transmisión) ni de edad de las personas (relevante para las series de fallecidos o las series de personas hospitalizadas). Además los parámetros del modelo son (como habitualmente en un modelo) fijos y constantes, cuando seguramente en la evolución de una pandemia cambian. Dicho esto, quizás para detectar evoluciones agregadas y efectos finales el modelo nos ayuda a conocer el impacto del aislamiento social. Y si piensas en términos cualitativos los resultados son los esperables (obviamente de acuerdo a los supuestos del modelo) y también de acuerdo a las evidencias empíricas que tenemos entre los escenarios del timing y la intensidad de intervención pública para el aislamiento (comparando por ejemplo Corea o Japón frente a Italia o España). Además, la simulación del modelo replica bastante bien la serie diaria de personas fallecidas totales tristemente observada en España.
Respecto a lo que comenta Anxo Sánchez, creo que es pertinente este post que enlazo debajo. Es sobre físicos, pero también aplica a economistas, supongo:
"The best thing you can do to fight COVID-19 is nothing. Stop writing that paper. Don't put it on the arxiv."
https://www.reddit.com/r/datascience/comments/fsfdn2/the_best_thing_you_can_do_to_fight_covid19_is/
Muchas gracias por compartir el análisis.
Seguramente no tengas tiempo, pero me lanzo a hacer un par de preguntas rápidas:
1) Los resultados parecen coherentes con otros modelos que se han publicado, en particular el de Imperial del 16 de Marzo.
¿Es así o calibrar el modelo para España aparecen conclusiones distintas?
2) Como explicas al comienzo del artículo, las medidas de distanciamiento social RETRASAN, pero no eliminan la epidemia (maldito virus). Según entiendo el análisis, cuantificas el efecto de aplicar medidas de contención permanentes (aunque relajáis esta premisa en las conclusiones).
¿Habéis extendido el modelo para estimar el aumento de contagio una vez se relajan las medidas de confinamiento?
Por ejemplo, ¿cuánto se tarda en colapsar los hospitales de nuevo si el confinamiento se acaba a las cuatro semanas? ¿y si es en seis? ¿en ocho? ¿cuánto tiempo es lo mínimo necesario para que la capacidad hospitalaria no se rompa?
Parece que nos enfrentamos a una decisión absolutamente cruel, pero inevitable: el colapso económico frente al impacto sanitario. ¿tenéis algún comentario a este respecto?
Gracias de nuevo y un saludo-
Hola, Segio, y gracias por tus comentarios. El trabajo de Imperial College presenta intervalos en sus predicciones y el límite superior de muertos a 31 de marzo es de unas 1000 personas. Lamentablemente se ha quedado muy corto (ayer la cifra era tristemente superior a 8000)... Nuestra calibración es muy sensible al número de contactos interpersonales diario y a la probabilidad de contagio en los contactos entre personas infectadas y personas sanas. La probabilidad de contagio la hemos calibrado para replicar la serie diaria de fallecidos acumulados en España, mientras que el número de contactos diarios lo reducimos de 25 a 3 al declararse el Estado de Alarma y comparamos la simulación con el escenario de no Intervención.
Respecto a tu segunda pregunta, el aislamiento retrasa la epidemia si existe antes de que comience (sección 4.1 del paper). Una vez que la pandemia ya está en marcha el aislamiento apenas retrasa los picos esperados, simplemente los reduce una barbaridad. Esta reducción es mayor cuanto más intensa es la intervención y, especialmente, cuanto antes se implementa. El problema que puede surgir aquí es que los gobernantes se resisten a tomar estas medidas por su efecto económico negativo y porque la ciudadanía no apreciará sus efectos positivos porque la pandemia sería muy leve. El segundo aspecto se lo tienen que comer los políticos porque les toca asumirlo si realmente toman decisiones para el bienestar social. Y respecto al primer argumento (usado por Trump)...
... creo que es totalmente equivocado. El retraso en la toma de medidas de aislamiento social hace que se extienda mucho más la pandemia, el sistema sanitario sufra una barbaridad y el retorno a la normalidad desde tan arriba de los picos va a costar mucho tiempo. Compruébalo en lo que le pasa a las líneas azules (retrasar 4 días el Estado de alarma al 18 de marzo) en la Figura 4 del paper respecto a la líneas rojas (Estado de alarma el 14 de marzo). Imagínate la debacle si retrasar las actuación más tiempo y además un porcentaje de tu población no disfruta de seguro de asistencia sanitaria. Espero equivocarme pero EEUU lamentablemente superará pronto a España e Italia en número de muertos (y posiblemente acabará siendo el país con mayor porcentaje de la población fallecida).
Una puntualización. He releído el trabajo del Imperial College al que hacía referencia el comentario y veo que el dato al que hacía referencia antes era el de fallecidos diarios cuando yo lo había interpretado como el dato de fallecidos acumulados hasta la fecha. Si buscamos este dato acumulado a 31 de marzo el modelo de Imperial College predice 7.700 muertos (Tabla 2 del paper). Nuestra serie estimada para el total de muertos a 31 de marzo era de 7.210 y el dato (oficialmente reportado ayer) fue de 8.189. Los modelos SIR predicen que las variaciones de esta serie acumulada (es decir, el número diario de fallecidos) se muevan ya a la baja porque los efectos del aislamiento provocado por el Estado de Alarma han de empezar a notarse dado que las infecciones graves por COVID-19 tiene en promedio una duración de 18 a 22 días. Confíemos que acierten los modelos esta vez.
Buenas tardes: muchas gracias por compartir vuestro trabajo. Una pregunta: cuando consideráis que el número medio de contactos es 3 si tiene en cuenta que en confinamiento esos contactos coinciden? Quiero decir que si en una vivienda viven cuatro personas el primero tiene contacto con los otros tres pero no hay 4x3=12 contactos sino la mitad. No se si es relevante o si quizá ese valor 3 es un promedio.
Muchas gracias y ánimo.
Hola, Juan, gracias por tu comentario. El número de contactos es por el que tiene una persona (el agente representativo) con el resto de personas en un día cualquiera. El modelo no permite diferenciar entre contactos repetidos a lo largo de los días, como los que se producen en una vivienda. Se podría extender el modelo con agentes heterogeneos por su tipología de contactos (lmuy interesante, por cierto). Respecto a la pregunta si cuentan los contactos de los miembros de una familia entre ellos, la respuesta es que sí. A modo de ejemplo, si en la familia representativa hay 4 miembros y el individuo 1 es el único que sale a hacer la compra y tiene un único contacto con la cajera del supermercado, tendríamos los siguientes contactos de la familia 4+3+3+3=13 y un contacto promedio por individuo de 3,25 .
Gracias por la entrada que tiene la virtud de ilustrar muy bien (sobre todo para los no especialistas en la materia) la evolución de la pandemos en función de parámetros básicos o el efecto de las medidas y dónde hubiéramos acabado de no haberse tomado. Sin embargo, como ya se ha dicho, no creo que las predicciones del modelo sean muy precisas. Dependen mucho de demasiados parámetros desconocidos y, en consecuencia, han de verse como una tendencia general. Valga como ilustración el punto 4: "Nuestro modelo predice que los máximos en el número de hospitalizaciones por coronavirus se observarán entre el 27 de marzo y el 4 de abril" Tengo la impresión de que es demasiado optimista.
En todo caso, no es un problema exclusivo de este modelo, sino de casi todos. Por ejemplo, el estudio de Imperial College habla de siete millones de contagiados en España y, aquí mismo, se mencionaba otro estudio en el que, a partir de encuestas, se hablaba de poco más de cien mil . En esos márgenes nos movemos.
He adelantado un modelo similar basado ne la misma metodología para Colombia, en efecto es sencillo pero muy practico para los fines requeridos. muchas gracias por el detalle de la explicación y la interpretación de variables. Muchas gracias!
Me parece un excelente trabajo, la estadística sé consume sí misma. Es una especie de vacuna, ya que los resultados del modelo y sus actualizacion, permiten ayudar al pronóstico en dónde apareció el Covid 19 desfasado. Poco tiempo tal vez unas semanas y logrando ganarle tiempo al tiempo. Saludos.
Los comentarios están cerrados.