"La respuesta de "sentido común" a la pregunta de .... ¿cómo se caracterizaría una economía motivada por la codicia y controlada por un gran número de agentes? sería, probablemente, el caos". Pero "hay una lista bastante impresionante de economistas, desde Adam Smith al presente, que han buscado probar que una economía descentralizada motivada por el auto interés y guiada por los precios es compatible con una disposición ordenada de los recursos económicos... y superior a una gran clase de sistemas alternativos"....
Arrow y Hahn, General Competitive Analysis. Holden Day, 1971 pp. vi y vii.
Arrow y Hanh
La oferta y la demanda en equilibrio parcial
La oferta y la demanda en equilibrio parcial es algo que todo el mundo entiende. Y mucha gente cree que sus propiedades son extrapolables a la economía en general y que con esto se puede entender cualquier problema económico. Spoiler. Pues no.
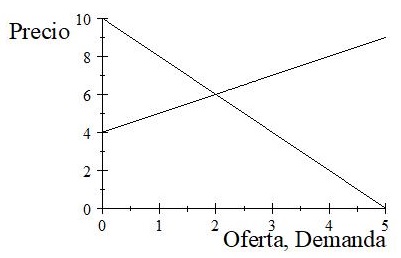
Todos somos familiares con el famoso gráfico.
Del que se sigue que existe un único equilibrio de mercado (con un precio de seis y dos unidades transaccionadas). Ese equilibrio es estable porque a un precio por encima de seis la oferta supera a la demanda y lo inverso ocurre cuando el precio es menor que seis. Además, movimientos de la oferta y la demanda tienen los efectos que la intuición sugiere.
El sistema en su conjunto
Si empezamos a pensar sobre el modelo anterior encontramos algunas cosas raras. Por ejemplo, ¿de dónde sale la renta con la que se compra ese bien? Y, si en el mundo hay una sola mercancía, ¿por qué se intercambia? Entonces comprendemos que, en realidad, el modelo anterior es una simplificación de un modelo en el que hay (por lo menos) dos mercancías. ¿Y qué pasa con el equilibrio en el mercado de la otra mercancía? Aquí viene en nuestra ayuda la ley de Walras que implica que, en un mundo con n mercados, si la oferta iguala a la demanda en n - 1 mercados, necesariamente el mercado restante está también en equilibrio.[2] Así que nuestro modelo anterior es un modelo de dos mercancías en el que el precio es el precio de esa mercancía relativo al de la otra mercancía (o relación de intercambio) y el equilibrio en ese mercado es suficiente para analizar el equilibrio de los dos mercados.
Haciendo alguna pirueta podemos interpretar el mercado de la figura como un mercado muy pequeño y el "otro mercado" como el resto de la economía. Pero el modelo anterior no es bueno si hay interacciones fuertes de ese mercado con otro, como en los mercados de energía o de alimentos. Y tampoco vale como una descripción del sistema económico porque la agregación de todos los demás mercados en uno es demasiada agregación. Resumiendo, el modelo de equilibrio parcial no es una buena guía para el análisis del sistema económico. Habremos de considerar modelos con más mercancías. Y eso hacemos.
Tres mercados... o más...
El bueno de Walras era consciente de que para analizar el sistema económico se necesitaban muchos mercados porque los sistemas económicos desde tiempos inmemoriales tienen muchísimas mercancías. Para ello amasó un porronazo de ecuaciones correspondientes a los mercados de bienes y de factores. Y las contó. Y como el número de precios relativos era igual al número de ecuaciones coligió que el sistema tenía, al menos, un equilibrio. Hoy casi cualquiera sabe que la igualdad entre el número de ecuaciones y el número de incógnitas no es ni condición necesaria ni suficiente de que un sistema de ecuaciones tenga una solución. Ejemplo, el sistema y = x + 3, x = y + 5 no tiene solución. ¿Qué podemos hacer?
Quiero remarcar que este problema no es una tecnicalidad. Si las ecuaciones que describen nuestro modelo de la economía no tienen solución, el modelo ES INCORRECTO. Y de él no puede extraerse conclusión válida alguna. Así, si suponemos que hay un número natural más grande que ninguno, llamémosle N, es fácil probar que tal número es uno (N ≥ N. N por hipótesis así que 0 ≥ N. (N-1) que implica N = 1 Tachannnnnn).
Ahora toca reflexionar ¿Por qué en el modelo de equilibrio parcial parece tan obvio que hay un equilibrio y que es único? Pues porque hemos pintado oferta y demanda astutamente de tal manera que para precios muy altos existe exceso de oferta y para precios bajos hay exceso de demanda. El teorema del valor intermedio nos garantiza que hay un precio para el que la oferta iguala a la demanda. Y ese teorema... ¿no vale en muchas dimensiones? Pues sí, pero no. Me explico.
El teorema del valor intermedio en n dimensiones se debe a Poincaré y Miranda y para nuestros nada siniestros propósitos puede enunciarse así:
Sean f1, f2, … fn funciones continuas de p1, p2, … pn cada una con rango en [0,1] y tales que, para todo i, cuando pi = 0, fi < 0 y cuando pi = 1, fi > 0.
Entonces hay unos p1, p2, …, pn tal que todas las fi = 0.
Interpretando los p como precios y las f como funciones de exceso de oferta, el teorema garantiza la existencia de unos precios tales que todos los mercados están en equilibrio. El problema son los supuestos.
La continuidad por ahora nos vale. Que el rango sea el intervalo cero uno es irrelevante. Cualquier otro intervalo (cerrado) nos serviría. Pero ¿por qué tiene que haber exceso de demanda de una mercancía cuando su precio es el mínimo sin importar cual sea el precio de los otros bienes? ¿Y si uno de esos precios es el salario de los consumidores de esa mercancía? En ese caso si ese salario es muy bajo la demanda de ese bien será cero. Y si esa mercancía no tiene utilidad alguna para sus poseedores estos la ofrecerán incluso si su precio es cero. En ese caso la función de oferta deja de ser univalorada (con un único valor en el rango para cualquier valor de los precios) para ser multivalorada. Glups! Y algunos de sus valores en el rango no cumplen los supuestos del teorema. Idénticas reflexiones se aplican a cuando el precio es el máximo. Pues puede ocurrir que los precios de los factores con los que se produce ese bien también sean máximos y sea imposible producir ese bien a beneficio no negativo.
Aún más canalla es el siguiente ejemplo:
Supongamos que existen una mercancía y un consumidor tales que ese consumidor tiene recursos iniciales sólo de esa mercancía, le gusta esa mercancía, pero no está interesado en el consumo de ninguna otra mercancía. Y hay otros consumidores que tienen recursos iniciales de esa mercancía, pero no están interesados en su consumo. Entonces no existe un equilibrio.
Prueba: Sea x la demanda de esa mercancía por parte de ese consumidor, w sus recursos iniciales de esa mercancía y W la oferta total de esa mercancía, mayor que w por hipótesis. Supongamos que hay un precio para el que ese mercado está en equilibrio p. Entonces la restricción presupuestaria de ese consumidor es px = pw. Nótese que p > 0 porque si no, ese consumidor demandaría cantidades arbitrariamente grandes de esa mercancía. Luego dividiendo la restricción presupuestaria por p, tenemos que x = w < W contradiciendo que el mercado está en equilibrio.
El ejemplo es, extremo, pero debe alertarnos para que no supongamos sin más que el equilibrio de mercado existe.
La solución... en el próximo capítulo...
[1]Agradezco a Carmen Beviá, Juan D. Moreno-Ternero y Jaume Sempere sus comentarios a una versión preliminar de este trabajo. Soy el único responsable de las opiniones aquí vertidas.
[2]La ley de Walras se prueba sumando las restricciones presupuestarias de todos los consumidores.




Hay 12 comentarios
Estimado Profesor Corchón,
¡Qué interesante esta entrada! Gracias por compartir.
Thomas Carlyle y el propio Samuelson bromeaban con la cuestión de que si le enseñas a una persona de la calle o a un loro a hablar en términos de oferta y demanda (enfoque de eq parcial) ya tenemos a un nuevo/a economista. No es una cuestión baladí, creo que el modelo de oferta y demanda marshalliano (o de equilibrio parcial) es el que más recuerdan la mayoría de estudiantes de economía, una vez que acaban sus estudios. Particularmente, aquellos/as que luego no hacen carrera académica.
Creo que el siguiente nivel de reflexión y divulgación es el de la propia definición, metodológicamente, de la noción de equilibrio en el análisis económico. Posiblemente los trabajos de Joan Robinson, Nicolás Kaldor, y el citado Frank Hanh serían muy convenientes de comentar.
Saludos.
Buenos días Alberto. Gracias por tu aportación y tus elogios.
Efectivamente el modelo de oferta y demanda de equilibrio parcial es uno de los mayores éxitos de la economía. Y no está exento de méritos. El problema es cuando se usa para cuestiones que no puede responder. Por poner un símil, hay telescopios para aficionados muy buenos pero tratar de hacer carrera académica en la astronomía con un telescopio casero es arriesgado por no decir otra cosa. El telescopio casero vale para lo que vale, pero nunca te va a detectar objetos estelares que son fundamentales para la comprensión del universo. Aquí un ejemplo de la utilidad de los telescopios caseros https://www.nobbot.com/entrevistas/joaquin-tapioles/ El problema es que hay gente que identifica "útil en algunas circunstancias" con "válido para cualquier cosa" y a veces cuando uno lee los análisis que se hacen de, por ejemplo, la economía española, piensa que es como enfrentarse a un león con un mondadientes, objeto también útil pero totalmente incapaz de hacer algo en esa circunstancia.
Estimado Luis, aún a riesgo de meterme en un jardín, quisiera compartir mi visión:
Cuando cada bien está disgregado entre distintos productores-receptores. Quedando la demanda parcialmente insatisfecha en la recepción, debemos llevar a cabo una distribución por intercambio o mercado.
El Mercado Natural (MN), representa una idealización de esta función primitiva. Lo explico muy bien AQUÍ.
El concepto de Equilibrio Natural (EN) que manejo, se aleja un tanto de la visión de equilibrio “convencional”. Mi modelo plantea dos agentes A y B. Cada uno con la capacidad de ofrecer y demandar un producto en exclusividad que al intercambiarse con el del otro, produce como resultado de la transacción, un EN, en el que oferta y demanda se anulan.
El problema es que tanto A como B, pueden mentir o ocultar información relevante al declarar en la transacción. En tal caso, las posibilidades se reducen a jugar con un posible excedente o escasez inducido por dicha falta de información. Y a partir de ahí las condiciones de juego cambian ostensiblemente. Obligando a reconsiderar la función primitiva del mercado, incorporando instrumentos de tipo matemático, principalmente probabilístico y estadístico, que nos ayuden a definir el equilibrio como el resultado de un tipo de estrategia concreta.
Buenos días Jordi.
Cuando existe información privada la tentación de mentir para aprovecharte es muy clara. Esta fue una de las motivaciones de Hurwicz para crear (con la ayuda de otros) el área del diseño de mecanismos de asignación de recursos también llamada implementación. Los mecanismos pueden ser directos (también llamados de revelación), en los que cada individuo anuncia su característica y abstractos en los que los anuncios pueden ser cualquier cosa (precios, cantidades, o levantar banderas,...).
Los resultados clásicos son 1) el principio de revelación: si hay un mecanismo abstracto que implementa ciertos resultados, existe un mecanismo directo que también los implementa. 2) En general no existe un mecanismo que implemente resultados eficientes. 3) Pero hay casos -que esencialmente requieren al menos tres agentes y algún tipo de relación entre la información de los agentes- en los que la eficiencia es alcanzable. Hace ya tiempo hice un survey de esta literatura https://www.eco.uc3m.es/temp/SURVIMPL.pdf
Estimado Luis, gracias por ponerme sobre la pista. Me abruma tu trabajo, carezco de la base matemática para entenderlo, además de la barrera del idioma, que no domino plenamente. Eso sin contar con la documentación y extensa referencia a autores y teorías que desconozco por completo.
Dicho esto, y suponiendo que todos respiramos el mismo oxígeno, que alimenta nuestras neuronas, me gustaría proponer humildemente un par de cuestiones, una mitológica y otra experimental.
M. Permíteme que nombre al Economista Omnisciente, figura de ficción que reúne las funciones que su nombre indica. Se trata de un ser “mitológico” que no puede ser engañado, y que por tanto es capaz de regular de forma eficiente cualquier transacción, al tener información completa en todo momento.
E. Ahora cambiemos al EO, por un algoritmo de consenso, no determinista, que se ejecute en tiempo real en una computadora cuántica o un cluster. Sumemos la capacidad de aprender y adaptarse a las diferentes entradas de datos en tiempo real, a través de APPs, que recogen las declaraciones de los agentes económicos involucrados en el experimento y valoremos los resultados.
Sí el ser mitológico era el planificador benevolente y perfectamente informado, concepto que se usa como un techo de lo que se puede alcanzar. El algoritmo (sin la connotación del AI ya que es más general) es el que yo propuse en uno de mis trabajos que no es el único sobre este tema https://www.eco.uc3m.es/temp/theory_JET_1997_ps.pdf
Estimado Luis.
Gracias por compartir tu trabajo. A mi me encantaría diseñar un algoritmo que tuviera en cuenta todos los parámetros que hemos resumido. No dispongo de mucho tiempo, y obviamente me faltan conocimientos, pero si llego a programar algo decente, es posible que lo publique en un repositorio de GitHub.
No me cansaré de repetir, el lujo que representa tanto este blog, como el conjunto de profesionales que hay detrás. Un fuerte abrazo.
Buenas noches Jordi y gracias por tus elogios.
La pregunta es ¿tiene algún interés científico o práctico el concepto de equilibrio en un sistema dinámico cuya evolución depende de las decisiones basadas en información parcial de múlltiples agentes sobre un sin número de variables?
El concepto de equilibrio estático es útil como una primera aproximación al conocimiento de un sistema. Es como una foto, quizá sólo una pintura, de la realidad que, efectivamente, es dinámica. Pero también hay conceptos de equilibrio dinámico en donde los agentes tienen unos planes y unas expectativas que, de alguna manera, se van cumpliendo. O si no lo hacen, los agentes los van revisando. Sería el equivalente a una película. Aquí puedes encontrar un libro sobre ello. El índice da una idea de lo que puedes encontrar https://www.theigc.org/wp-content/uploads/2016/06/acemoglu-2007.pdf
Luego también hay una dinámica basada en el ajuste hacia el equilibrio estático. Y que en experimentos parece funcionar bastante mejor de lo que nosotros mismos creíamos, ver por ejemplo https://www.aeaweb.org/articles?id=10.1257/aer.101.7.3196
Muchas gracias. Conozco, bien es cierto que por encima, el paper "Extreme Walrasian Dynamics: The Gale Example in the Lab." de Crockett, Oprea y Plott y no me parece que sea una linea de investigación muy prometedora. El libro de Acemoglou va en otra dirección, en mi opinión, mucho más interesante. En cualquier caso, muchas gracias por su información.
Si, yo también lo pienso así. De hecho Acemoglu ha sido uno de los pocos economistas que ha dado un giro radical a nuestra disciplina, poniendo la explicación de los fenómenos históricos en la primera fila de nuestras agendas. El problema es que, en su opinión, las instituciones son la raíz de todo y cuando dice instituciones quiere decir las anglosajonas, o sea separación de poderes, elecciones, derechos de propiedad bien defendidos etc. En su opinión esa es la razón por la que la revolución industrial ocurre en Inglaterra y luego el testigo pasa a USA. Aquí ya hay un problema porque la Alemania del Kaiser no tenía unas instituciones especialmente encomiables y sin embargo llegó a ser competidora de los británicos (y muy posiblemente, si rusos y norteamericanos no se hubieran cruzado en su camino, hubieran acabado derrotándola militar y económicamente). ¿Cómo se explica eso? Ahora con el caso de China y el resurgimiento de Rusia, ambas naciones con unas instituciones muy poco recomendables, esa teoría, en mi opinión, se hace difícil de mantener. El capital humano. a mi entender, es la variable clave.
Los comentarios están cerrados.