Todas los años sobre estas fechas la prensa se inunda de artículos dedicados a la Lotería de Navidad. Hay varios temas que se repiten. Muy a menudo se afirma que las provincias más afortunadas son Madrid y Barcelona, porque es donde más veces ha tocado el gordo. También hay quien recomienda peregrinar a Sort con la esperanza de que los billetes vendidos por La Bruixa d'Or traigan más fortuna. Curiosamente, estos argumentos no tienen en cuenta el gasto en lotería ni tampoco la estrategia de la Bruixa d’Or de comprar unas pocas series del mayor número posible de números, de manera que se maximice la posibilidad de vender al menos alguna serie de uno de los premios grandes. ¿Podrían estos mitos sobrevivir a un análisis un poco más sofisticado del cálculo de las posibilidades que tiene cada provincia de ganar en la Lotería de Navidad?
Los datos muestran que existen algunas provincias con mucha suerte, pero no se trata ni de Madrid, ni Barcelona, ni Lleida. Por cada euro gastado en Lotería de Navidad en los últimos 25 años Soria ha recibido unos tres euros en premios, Huesca unos dos euros y medio y Segovia un euro y medio, cantidades muy superiores a las recibidas por Lleida (un euro ganado por cada euro gastado), Barcelona (80 céntimos) o Madrid (67 céntimos). Además de Lleida, durante este período hay otras tres provincias que han quedado a par (Alicante, Burgos y Granada), mientras que el resto ha tenido pérdidas. Las provincias más desafortunadas han sido Ávila, Huelva y Guadalajara, donde en los últimos 25 años no ha tocado ni un triste décimo de alguno de los tres primeros premios de la Lotería de Navidad.
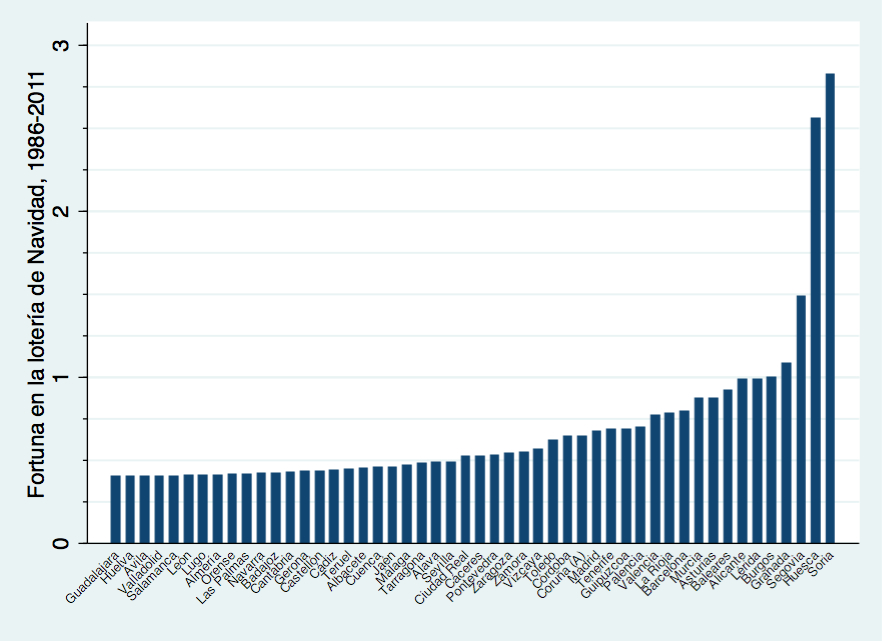
Otro mito es que la lotería disparará el consumo en la localidad ganadora. Si bien esto es cierto en épocas de bonanza económica, la evidencia de años recientes sugiere que en época de crisis la propensión al consumo de los ganadores podría ser más baja. Por ejemplo, no parece que el Gordo de 2011 haya tenido un impacto muy significativo sobre la venta de coches en la provincia ganadora, Huesca, donde las pasadas navidades cayó una lluvia de unos 720 millones, unos 3,000 euros por habitante. En 2012 la venta de coches cayó en un 20.6%, cifra igual a la media nacional (-20.4%). Esto contrasta con los incrementos en las ventas de coches que se han observado en el pasado en las provincias de características similares que han ganado el Gordo. Tanto en Segovia (año 2000, 2000 euros por habitante en premios) como en Soria (año 2006, 4,000 euros por habitante en premios), la venta de coches aumentó en un 10%, mientras que en el resto de España esos años las ventas se mantenían constantes (2001, +0.3%; 2007, -0.6%).
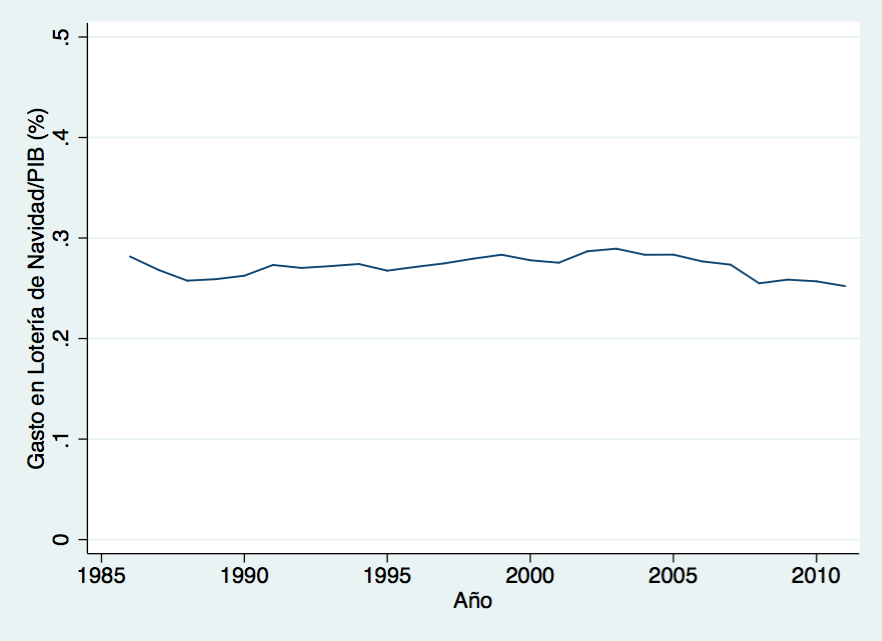
Un tema que todos los años atrae la atención de los periodistas es la evolución de las ventas de la Lotería de Navidad. En general los artículos se dividen entre análisis apocalípticos, que preven un descenso de hasta el 40% en las ventas, y artículos hiperoptimistas que auguran que la crisis disparará las ventas. La realidad será probablemente mucho más prosaica. No existen precedentes de variaciones tan dramáticas como las anunciadas. La evolución del gasto de navidad en las últimas décadas sugiere que la lotería es un bien normal cuyo consumo se sitúa en torno al 0.25% y el 0.28% del PIB.
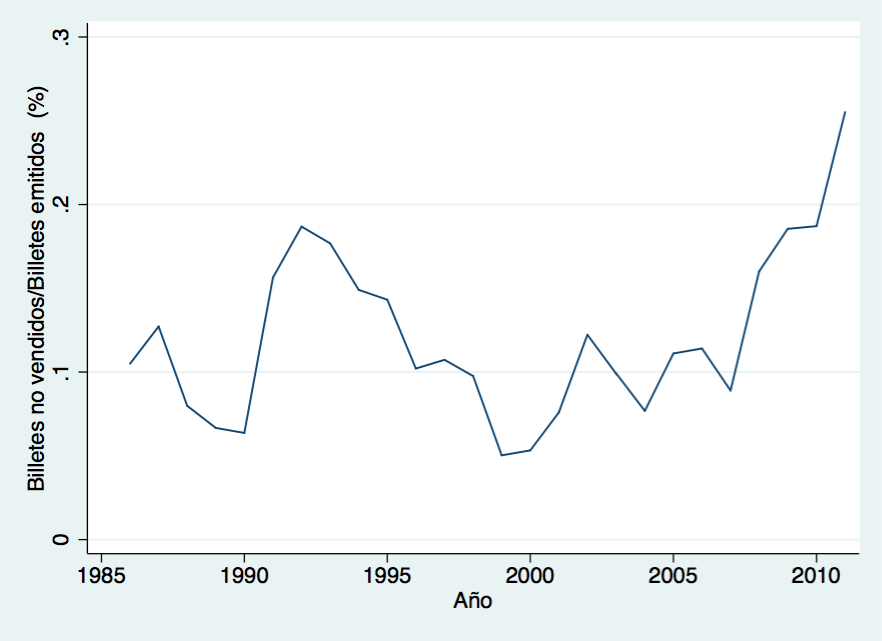
Curiosamente, aunque el número de billetes vendidos no ha variado excesivamente en los últimos años - una caída del 6% entre 2007 y 2011 - lo que sí que ha aumentado considerablemente es el número de billetes no vendidos. Si hace unas cinco navidades únicamente el 10% del total de billetes emitidos quedaba sin vender, en la actualidad la cifra es cercana al 25%. Este aumento en el número de billetes no vendidos se debe en gran parte al reciente incremento en la cantidad de números sorteados, de 85,000 a 100,000, que coincidió con un aumento en la cuantía del primer premio (de tres a cuatro millones por serie) y una ligera reducción en el número de series.
La probabilidad de que en el sorteo de este sábado el Estado se lleve alguno de los premios grandes es relativamente alta, lo que supondría un ingreso muy substancial para las arcas públicas. Si, por ejemplo, ganase el Gordo (25% de posibilidades), el gobierno ingresaría un total de 1135 millones de euros, incluyendo los 720 millones de euros del primer premio. Sin embargo, también cabe la posibilidad de que no tenga tanta suerte en el sorteo y los ingresos públicos sean inferiores a lo esperado. Si el Estado no gana ninguno de los cinco primeros premios los ingresos del gobierno serán únicamente de unos 416 millones. Es decir, aunque el Estado tiene siempre la misma ganancia esperada (un 30% del gasto, unos 800 millones este año), al aumentar el número de billetes no vendidos aumenta el riesgo que está asumiendo en el sorteo. ¿Será que a nuestro Gobierno le gusta jugar a la lotería?

Hay 25 comentarios
Hola Manuel, muy interesante.
En todo caso, en la enumeración de provincias extremas, quizás tendrías que explicar explícitamente que hay un tema de valores extremos para poblaciones pequeñas (por mayor varianza esperada)
Gracias Roque, debería haber sido más cuidadoso para no dar lugar a ningún equívoco. ¡Ya he visto un tweet que recomendaba comprar lotería en Soria! 🙂
Quizás no habría estado mal mostrar también que la autocorrelación de la suerte es nula, por mucho que algunos se empeñen en comprar lotería en los lugares donde ha tocado recientemente.
La verdad es que la desviación de Soria y Huesca (y en menor medida Segovia) respecto de las demás es muy significativa, viendo la gráfica parecería que ahí sí hay suerte especial.
Me da que puede ser un efecto del reparto de una distribución uniforme (que a fin de cuentas eso se supone que es la lotería) sobre subpoblaciones asimétricas. En la lista de 50 provincias ordenada por población, Soria es la 50, Segovia la 48 y Huesca la 43. Es decir, están (relativamente) poco pobladas, así que si tienen que salir outliers lo lógico es que fueran esas, puesto que en las más pobladas los efectos de los outliers se diluyen y tendremos regresión hacia la media. La "media" sería el porcentaje que la lotería dedica a premios, un 70% según la Wikipedia. Lo cual encaja bien con las ganancias esperadas de las provincias más pobladas, Madrid (67 céntimos) y Barcelona (80c).
Por el otro lextremo, la que menos suerte tiene (Guadalajara) es la 42 por población, así que podemos estar viendo el mismo fenómeno de "outlier saliency", pero por el lado opuesto.
En resumen, que todo parece corroborar el carácter auténticamente aleatorio de la lotería, a pesar de la impresión a primera vista. Quizás si se dividiera en vez de por provincias por subáreas geográficas de igual población el efecto "suerte especial" de Soria y Huesca desaparecería.
Pvn,
Exacto, la distribución es consistente con una asignación aleatoria de los premios en la que, como muy bien apuntas, las poblaciones más pequeñas son las que más probabilidad estadística tienen de destacar como outliers y la media es 0.7, el porcentaje asignado a premios.
Si tuviésemos unidades geográficas de tamaño similar, la distribución sería un poco menos "skewed".
Teruel también existe.
Dado que entre los jugadores es habitual comprar (o encargar) lotería a Madrid, Barcelona o lugares donde se viaja (por eso empezó a venderse Lotería de Navidad en verano, recuerdan), el denominador correcto para casos como Madrid, Barcelona, Alicante o Mallorca no sería la población ¿no creen?
Jaime,
Gracias por el comentario. Tienes razón, hay gente que compra lotería en otras provincias. En este caso no afecta al computo de la variable "suerte de la provincia". Por no alargarme, no expliqué con detalle como se construyó esta variable. El denominador incluye los billetes de lotería comprados en una determinada provincia, tanto por residentes en esa provincia como por residentes en otras provincias, y el numerador incluye los premios recibidos por esos billetes, independientemente de donde habite el comprador. Por otro lado, los datos de contabilidad nacional, donde se proporciona información acerca de donde se cobraron los premios, sugieren que más o menos el 95% corresponden a habitantes de la misma provincia donde se vendió el billete.
"La lotería es el impuesto que grava el desconocimiento de las matemáticas". Adam Smith.
Victor,
Algún colega mío también dice que es un impuesto a la estupidez, pero creo que en el caso de la Lotería de Navidad se equivoca. Nuestro bienestar depende en gran parte de nuestra renta relativa, por lo que podría ser una estrategia óptima comprar el mismo número que compran todos nuestros amigos. No querríamos que nos ocurriera lo mismo que le ocurrió el año pasado a un tipo llamada Costis Mitsotakis, el único habitante de un pueblo de Huesca que no había comprado un billete del gordo.
Manuel, vienes a confirmar que en España el deporte nacional es la envidia... Je, je.
"La lotería es el impuesto de los tontos" y a partir de enero 2013 más que nunca
La forma mas segura de que te toque es ...NO JUGAR y dedicar el dinero a una imposición a plazo. Con la magia del tiempo y del interés compuesto, en 20 años una pasta.
Saludos.
Todo apunta a que la temperatura media en la provincia en el momento del sorteo es la variable que explica la probabilidad de éxito en la lotería -.)
... y que el ratio premios totales/gasto total es una cosa, mientras que el ratio premios por persona/gastos por persona a lo mejor reflejaría mejor las ganancias relativas de las personas que vivimos en esos fríos y no muy habitados lugares.
Jorge,
Tienes razón, no me había dado cuenta de que en las tres provincias más afortunadas suele hacer un frío que pela en invierno. Yo ahora mismo estoy en San Petersburgo, donde la previsión del tiempo para este fin de semana es que nos pongamos a -31 grados C, ¡así que me tiene que tocar seguro! 🙂
Con la segunda parte de mi razonamiento he cometido un fallo matemático de principiante. Se me ha ocurrido hablar del ratio "premios por persona/gastos por persona, cosa que es exactemente el que se maneja en el gráfico: (gastos/premios).
En realidad, lo que estaba pensando es que en esos lugares puede haber bastante gente en la cola de la distribución correspondiente a un nivel de gasto bastante alto en lotería (no se en otros sitios, pero ahí conozco bastantes outliers de esos). Es decir, que son unos outliers, pero su dinero les cuesta.
Jorge,
Gracias por la aclaración! Existe bastante información acerca de la distribución del gasto en lotería de navidad en unas encuestas que realiza el CIS cada tres o cuatro años. Como se puede ver en la Figura 4 de este artículo, en general no hay muchos outliers. El 75% de la población compra algún billete, el gasto medio está en torno a los 70€, y menos del 5% gasta más de 150€. Lo que por desgracia no indica la encuesta es cuanto gasta de media este grupo de "grandes" jugadores.
Aunque no lo diga el artículo, entiendo que las desviaciones de Segovia, Huesca y Soria se deben, cada una, a algún acontecimiento puntual, como que cayeran muchas series del gordo en un año concreto. Si en 2006 el gordo hubiese caído Teruel en vez de en Soria, o en Guadalajara en vez de en Huesca, se habrían intercambiado en la gráfica.
Lo digo por si alguien tiene deseos de salir corriendo hasta Soria 😀
Casty,
Muchas gracias por el comentario, la aclaración es muy oportuna a la vista de algunos tweets. Creo que, por deformación profesional de economista, omití decir que no trataba de crear un nuevo mito. Simplemente el azar probabilístico hace que algunas provincias acumulen más premios que otras (Soria en los últimos 25 años acumula un primer premio, un segundo, y dos terceros, a parte de algún pellizco más). Por cierto, estadísticamente la suerte que ha tenido una provincia en el pasado no tiene ningún poder predictivo sobre la suerte que tiene en los sorteos sucesivos, pero sí que causa un ligero aumento en las ventas de lotería de navidad en la provincia. Este es un fenómeno que ha sido también descrito en otros países ("Gambling at Lucky Stores: Empirical Evidence from State Lottery Sales").
http://sociedad.elpais.com/sociedad/2012/12/21/actualidad/1356094568_580787.html
mito o realidad?
Daniel,
No sé cuantos billetes de lotería compra Fabra cada navidad pero sería interesante calcular cuál es la probabilidad estadística de que exista una persona con tanta suerte. Pero si te soy sincero lo que más me impresiona no es su capacidad de ganar a la lotería, sino que además es capaz luego de ganar las elecciones! (espero que nadie se ofenda por este comentario, si es así pido disculpas)
Una pregunta... ¿Pueden fenómenos como Carlos Fabra alterar de forma significativa esta distribución? ¿Estudiar de forma pormenorizada cada sorteo, serie, provincia... no permetiría encontrar pautas que sirviesen como indicios de actividades de blanqueo?
Aunque supongo que los datos geográficos se refieren a la administración de loteria y no al domicilio de los ganadores y, por lo tanto, sería imposible trabajar con estos datos.
Hola Carles,
Exacto, la información que yo observo es únicamente la administración de lotería. Creo que en España las autoridades no recogen de una manera sistemática información acerca de quien ha sido premiado, pero puedo equivocarme. Mi impresión es que el blanqueo es un fenómeno menor, pero no dispongo de evidencia empírica. Desde luego, si hubiera información, sería interesante comprobar si la distribución de décimos en los primeros premios es similar a la distribución de décimos entre los premios menores (la idea que tengo en mente es que sería extraño que los ganadores del primer premio tuvieran en general varios décimos y, por el contrario, los premios menores estuvieran muy repartidos).
Muy buen articulo, directo y al grano.
Hay una literatura relativamente reciente en la que las loterias sirven para aliviar problemas de restricciones de liquidez. La idea es sencilla, algunos españoles tienen unas ideas buenisimas para montar un negocio, desde un estanco a un restaurante o lo que sea, pero el sistema bancario no es perfecto y no puede distinguir buenos proyectos de los malos, además los españoles no tenemos mucho colateral que poner para señalizar lo bueno de nuestra idea... Pues bien, los que tienen una buena idea gastan el poco dinero que tienen para el colateral en billetes de loteria, a los que les toque el gordo pueden llevar a cabo su proyecto. Como en esos casos el pago es mayor que el premio del gordo, porque la idea era muy buena y genera mas que la inversion inicial, incluso para individuos aversos al riesgo, esa es una buena idea.
Como anecdota, la madre de un amigo portugues gano el equivalente a la quiniela en Portugal hace muchos años. Con ese dinero pudo ir a la universidad, estudiar una carrera y tener un buen trabajo de maestra. En ese caso el pago de la inversion tambien fue mayor que el valor intrinseco del premio.
Seria interesante ver como cambia el destino del dinero del premio con el ciclo economico. Cuantos "para tapar agujeros" vs "para montar un estanco" hay en años de crisis y en años de bonanza.
Jose,
Muchas gracias por tus comentarios, muy oportunos. Precisamente hace unas semanas descubrí esta literatura que comentas a través de un artículo de Sarah Smith y coautores (Do Consumers Gamble to Convexify?). Es una idea interesante. Aquellos individuos que tienen restricciones de liquidez y desean adquirir un bien de consumo o inversión indivisible, podrían intentar vencer estas restricciones a través de su participación en un sorteo de lotería. Lo que no estoy muy seguro es su relevancia en el contexto de la lotería de navidad, donde parece que el aspecto social es el dominante, tal y como explica Roberto Garvía en un estupendo artículo. Quizás este argumento podría afectar proporcionalmente a más gente en los sorteos de lotería nacional que se celebran a lo largo del año.
Y gracias también por la última idea. Hemos comenzado hace poco a explorar a qué se destina el premio en función del ciclo económico. Los datos no son muy precisos, pero intentaremos ver si es posible profundizar en la dirección que señalas.
El aumentar la cantidad de números no sorteados sin necesidad no es más que un impuesto esperado sobre las retribuciones de los premios de un 17% o así. Dentro de nada otro 20% de IRPF... Manda óvalos, como dijo Federico. Cada vez interesa menos jugar.
Juan,
No exactamente. Hace un par de años se aumentó el número de billetes de 85.000 a 100.000, pero se reestructuró la cuantía de cada premio de forma que se mantuviera la norma de que el 70% de la recaudación se dedicara a premios. El valor total de los billetes puestos a la venta este año era de unos 3600 millones de euros y el total destinado a premios ascendía a 2520 millones (el 70%). Pero en la práctica no se suelen vender todos los billetes. Por ejemplo, este año se vendieron 2466 millones, el 68.5% del total, lo que supone que se quedaron sin vender el 31.5% de los billetes. El Estado no tuvo suerte con el sorteo. Se habían vendido el 80% de los décimos del número que recibió el primer premio y el 100% del segundo premio. Si suponemos que el 68.5% de los premios menores ha recaído en billetes que habían sido vendidos, en total se han repartido en premios unos 1880 millones, lo que equivale al 76% del gasto en lotería. El Estado ha dejado de ganar unos 150 millones por su mala suerte. Pero vaya, ha sido simplemente una cuestión de azar. Si hubiera tocado algún número de los llamados "feos", que se suelen quedar sin vender, el Estado se habría llevado probablemente una proporción de los premios mayor de lo esperado. En definitiva, como indicábamos en el post, al aumentar la proporción de billetes sin vender, en parte por la caída en la demanda y en parte por el aumento en la oferta, tiende a aumentar la varianza en la ganancia del Estado.
Los comentarios están cerrados.