 La reciente y fulminante quiebra y no menos fulminante desaparición del Banco Popular me han hecho pensar, desde mi perspectiva de físico e ignorante total, en la estabilidad del sistema financiero. Hablé de este tema y de cómo las ciencias de la complejidad pueden aportar cosas en el terreno de la regulación en NeG hace algo más de un año, pero ahora he visto algunos trabajos que profundizan en esta línea de investigación y que este "incidente" me empuja a compartir con usted, amigo lector. En concreto, para el caso del Popular, lo que me inquieta es si conociendo el estado de este Banco antes de la quiebra, y el del Santander después de la compra, podemos saber el efecto de este proceso sobre todo el sistema. Y lo que leo, y cuento debajo, me dice que no.
La reciente y fulminante quiebra y no menos fulminante desaparición del Banco Popular me han hecho pensar, desde mi perspectiva de físico e ignorante total, en la estabilidad del sistema financiero. Hablé de este tema y de cómo las ciencias de la complejidad pueden aportar cosas en el terreno de la regulación en NeG hace algo más de un año, pero ahora he visto algunos trabajos que profundizan en esta línea de investigación y que este "incidente" me empuja a compartir con usted, amigo lector. En concreto, para el caso del Popular, lo que me inquieta es si conociendo el estado de este Banco antes de la quiebra, y el del Santander después de la compra, podemos saber el efecto de este proceso sobre todo el sistema. Y lo que leo, y cuento debajo, me dice que no.
En febrero pasado, Marco Bardoscia, Stefano Battiston (un físico reconvertido a catedrático de finanzas en Zürich del que también hablé aquí), Fabio Caccioli y Guido Caldarelli publicaron este artículo en Nature Communications sobre cómo los sistemas financieros pueden evolucionar hacia situaciones inestables. El artículo es un poco técnico, tanto desde el punto de vista de las herramientas financieras como desde el punto de vista matemático, por lo que no voy a entrar en demasiado detalle de lo que hacen, aunque sí creo que puedo dar una impresión general y remitir a los interesados en profundizar al trabajo original. Aprovecho para pedir disculpas a los auténticos expertos si digo cosas inexactas o hago malas traducciones de términos financieros, y agradeceré mucho si me corrigen en los comentarios.
La idea central de este trabajo, como de la mayoría de trabajos sobre complejidad y finanzas, es construir una red en la que los nodos son los bancos, conectados por ciertos criterios. Aquí nos preocupan lo que se viene considerando como los dos mecanismos principales de propagación de problemas financieros: el contagio de falta de liquidez (illiquidity contagion) y el deterioro de activos interbancarios (interbank assets). En el primer caso, si un banco cree que otro al que ha prestado dinero puede tener problemas de liquidez, intentará recuperar su dinero, haciendo que a su vez el segundo banco recupere el suyo de otros sitios, transmitiendo así el problema. En el segundo, el problema aparece por un cambio en el valor de esos préstamos o acciones al empeorar las perspectivas del segundo banco, con el consiguiente impacto en la hoja de balance del banco (lo que se conoce en contabilidad como mark-to-market). Ambos mecanismos están relacionados y por ello los autores del artículo se centran en el primero (véase por ejemplo aquí para una discusión más amplia) para construir las conexiones entre los bancos de nuestra red.
El lector no interesado en la matemática puede saltarse este párrafo (bajo mi mirada ceñuda, eso sí) y asumir que podemos saber cuándo una red dada es inestable mediante un algoritmo. Para el que quiera tener una pincelada de lo que se hace, es necesario recurrir al álgebra lineal (que como muy bien nos explicó Jesús aquí es uno de los pilares de las matemáticas de la economía) para describir cuantitativamente nuestra red, mediante el concepto de matriz de apalancamiento (leverage matrix). Si tenemos n bancos, construimos una matriz n x n en la que el elemento ij es la relación entre la exposición del banco i al j y el capital propio (equity) del banco i. Bajo hipótesis no muy exigentes, se puede ver que la pérdida de capital propio de un banco i se puede obtener a partir de esta matriz y de las probabilidades de quiebra en función de las pérdidas patrimoniales de todos aquellos a los que está expuesto. Si además suponemos que estas probabilidades son funciones convexas de las pérdidas, llegamos a que la estabilidad del sistema viene dada por los mayores autovalores de la matriz de apalancamiento y de otra corregida por las tasas de recuperación (recovery rates) o fracción de activo recuperable en caso de quiebra de cada banco. De hecho, la ecuación que deducen los autores es

donde h representa las pérdidas de capital del banco i, p la probabilidad de quiebra, y la "lambda mayúscula" es la matriz de apalancamiento corregida que mencionaba. Y con esto acabo las matemáticas, si bien añado una nota técnica al final que puede interesar a muchos lectores.
Vemos entonces que si conocemos los bancos que nos interesan y sabemos la exposición de unos a otros (¿lo sabemos? Déjeme, querido lector, que posponga esta pregunta para el final), podemos saber si el sistema es estable o no. Por estable entendemos, como en cualquier sistema dinámico, que si el sistema es alterado en alguno de sus componentes de manera no muy fuerte, recuperará el estado de partida; inestable, en cambio, es aquel sistema que al ser alterado ligeramente evoluciona alejándose del estado de partida y acabando en otro que puede ser muy diferente. Llegamos así a lo interesante: con este resultado, los autores del artículo muestran que, sin que cambie el apalancamiento de ninguno de los bancos, un sistema financiero estable puede pasar a ser inestable (o viceversa) si cambia el número de bancos del sistema (en particular, si crece, añadiendo bancos a la red) o si cambia la estructura de préstamos entre ellos (lo que conlleva cambios en el peso de los enlaces de la red). En la siguiente figura recojo un ejemplo:
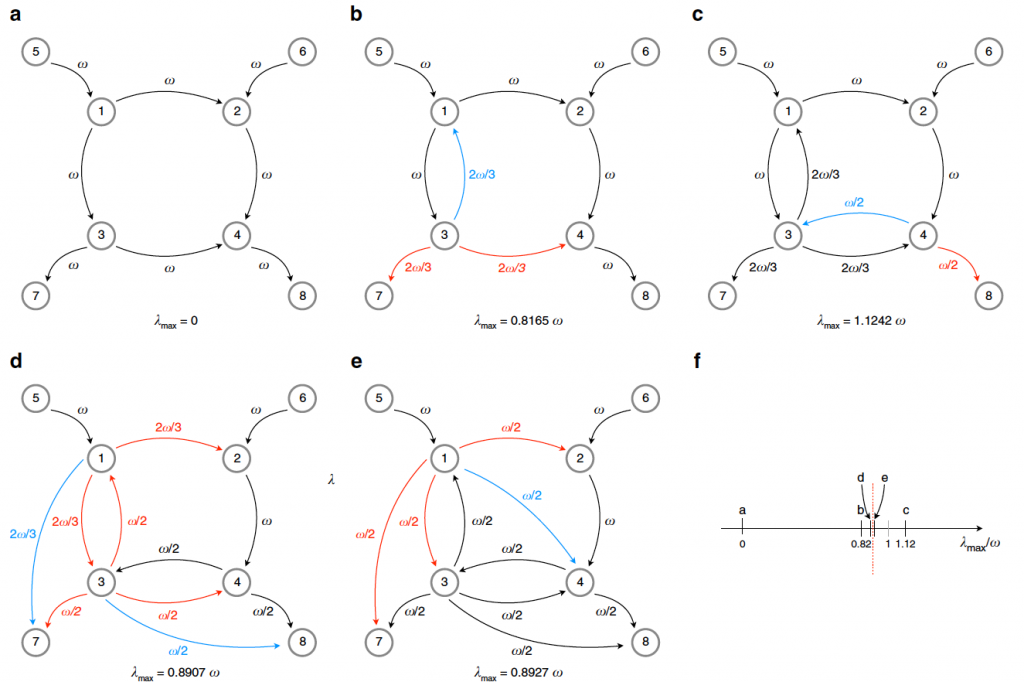
La situación en a corresponde a un sistema bancario con 8 bancos, y las flechas indican la exposición de unos a otros. Por simplicidad (pero que no afecta a las conclusiones generales) supondremos que son iguales y que el apalancamiento es el mismo para todos. Es importante observar que la red en a) no tiene caminos cerrados (grafo acíclico dirigido) y por tanto su máximo autovalor es 0, y es una red estable. En este ejemplo, solo vamos a ir añadiendo enlaces sin cambiar el apalancamiento total: así en b vemos que el banco 3 redistribuye su exposición, diversificandola incluyendo al banco 1 cuando antes solo tenía al 7 y al 4. Ese cambio ya hace variar el máximo autovalor, aunque la red sigue siendo estable. Este tipo de procesos nos lleva a redes como la c o la e que son inestables, debido a la redistribución de los apalancamientos. Es decir, los datos individuales de los bancos no son suficientes para determinar la estabilidad del sistema, y cuando un banco se expone a otro sin tener en cuenta la relación de este con los demás puede alterar la estructura de todo el sistema. El mecanismo básico (pero no el único) es la aparición de ciclos, que hacen que una vez que se inicia un proceso de contagio se vaya amplificando al recorrer el ciclo una y otra vez. Esto ocurre también en simulaciones más realistas:
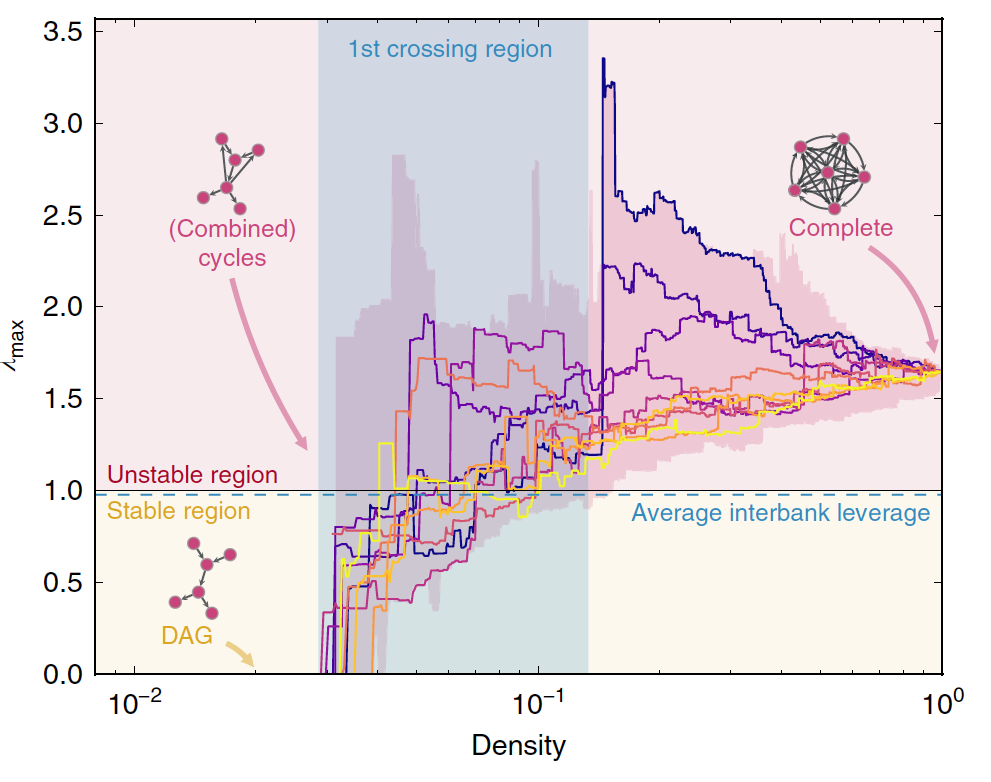
En la figura vemos simulaciones con los 50 bancos europeos más importantes (datos de 2013) en las que se ve como a medida que aumentamos la densidad de conexiones (con un algoritmo que modifica las exposiciones de todos sin afectar a sus balances), es decir, nos movemos hacia la derecha, los autovalores van variando, entrando y saliendo de la zona estable hasta acabar siempre en la inestable a partir de un cierto número de conexiones. Las consecuencias prácticas de esto son importantes: citando a los autores (la traducción es mía):
Actualmente, la estabilidad del sistema financiero se analiza mediante los test de estrés, que son procedimientos largos (...) que requieren modelos econométricos detallados y la cooperación de los bancos. Aunque son cada vez más sofisticados, los test de estrés normalmente asumen que los bancos son instituciones aisladas y desprecian las consecuencias de la propagación de los problemas por la red de contactos. Nuestra propuesta es mucho más ágil en tanto en cuanto permite establecer la estabilidad del sistema (...) utilizando la información de las exposiciones mutuas entre bancos (que normalmente el regulador conoce), los capitales propios (que son públicos) y las tasas de recuperación (que se pueden estimar) (...) aparte de que siempre se pueden estudiar muchos escenarios correspondientes a distintas tasas de recuperación).
Creo, desde un punto de vista que insisto es muy ignorante, que este tipo de trabajos apuntan a maneras que, si no me atrevo a llamarlas correctas, si diré que son complementarias de lo que se hace hoy en día para estudiar la situación del sistema financiero. Los ejemplos de casos que darían los mismos resultados en test de estrés que discute el artículo, como los de arriba, y que unos corresponden a redes estables y otros a inestables, hacen necesario a mi juicio darle una vuelta a cómo estamos estudiando estos problemas, y a darnos cuenta de que en un sistema complejo, lo que le ocurre a uno de los componentes puede afectar a todos de maneras y por mecanismos nada triviales (hasta que uno se da cuenta de ellos, claro está).
Ah, y una última nota que dejé pendiente sobre los datos: aparte de lo que ya he dicho de que en muchas ocasiones están disponibles, la propia ciencia de la complejidad nos proporciona métodos para recuperar datos y conexiones no conocidas en redes a partir de unos pocos que sí se conocen. Por ejemplo, mi co-autor Giulio Cimini y colaboradores muestran en este artículo que es posible reconstruir con mucha precisión una red (bancaria o de cualquier otra cosa) teniendo una idea de las propiedades generales de los nodos, y conociendo unas pocas conexiones (véase también este trabajo reciente en el que se compara este método con muchos otros y se analiza cuáles son mejores en función del tipo de datos disponible y de lo que se quiere). Así que el que no se tengan todos los datos no es una excusa para no empezar a aplicar en serio este tipo de ideas a la hora de entender la estabilidad de nuestros bancos. Me parece un asunto lo suficientemente serio como para atacarlo con toda la artillería posible, aunque algunos cañones vengan de una panda de físicos asilvestrados. Y en particular, dada la magnitud de los bancos involucrados en la desaparición del Popular, creo que no estaría de más echar un vistazo a ver qué ha cambiado en el sistema bancario español y europeo desde esta perspectiva, que lo mismo nos llevamos una sorpresa, y quizás no agradable.
Nota técnica: la clave del artículo es la ecuación del sistema dinámico que derivan los autores y que pongo más arriba (y en la que creo que hay una errata, el miembro de la derecha debería poner h(t) y no h(1)), y para entender su aplicabilidad bien hay que ir al material suplementario del artículo. Por otro lado, hay un trabajo de 2015 de Acemoglu, Ozdaglar, y Tahbaz-Salehi que utiliza ideas similares y se concentra en analizar los puntos fijos de la evolución de su sistema dinámico. En este sentido, en el artículo que comento aquí interesan más las perturbaciones en torno a los puntos fijos, lo cual es importante para comparar las conclusiones de ambos trabajos, que por otra parte no son tan diferentes.
