Daniel Oto-Peralías y José Antonio Robles-Zurita
En esta entrada abordamos una cuestión de especial relevancia en estos momentos en los que los gobiernos autonómicos están endureciendo las restricciones para aplanar la curva de contagios y hospitalizaciones. Las restricciones adoptadas consisten en cierres perimetrales, suspensión del ocio nocturno, límites a la hostelería, etc. A diferencia de las medidas tomadas en primavera, existe cierto consenso en que la educación no debe parar. En particular, hasta ahora se está tratando en la medida de lo posible de mantener la presencialidad en los niveles de infantil, primaria y secundaria. Ello se justifica principalmente, por un lado, en la importancia de la educación y las consecuencias negativas de la no presencialidad y, por otro, en que el efecto sobre el aumento de contagios es moderado. A continuación, examinamos precisamente esto: si el comienzo escolar a principios del pasado septiembre ha acelerado la propagación del coronavirus.
La evidencia disponible sobre el efecto de la reapertura de los colegios en la pandemia es todavía escasa. Por un lado, existen estudios observacionales de seguimiento de poblaciones escolares (ver una discusión aquí y aquí). En otro tipo de estudios, el uso de modelos epidemiológicos sirven para realizar simulaciones (por ejemplo aquí). Estos estudios tienen la limitación de que no se basan en inferencia causal o no hacen uso de datos recogidos en el contexto real en el que se imparte docencia. Si bien existen algunos análisis empíricos (ver aquí), la evidencia aportada podría no ser comparable entre distintos momentos (las medidas de seguridad han cambiado a lo largo de este año) o entre países (el contexto educativo y social es distinto).
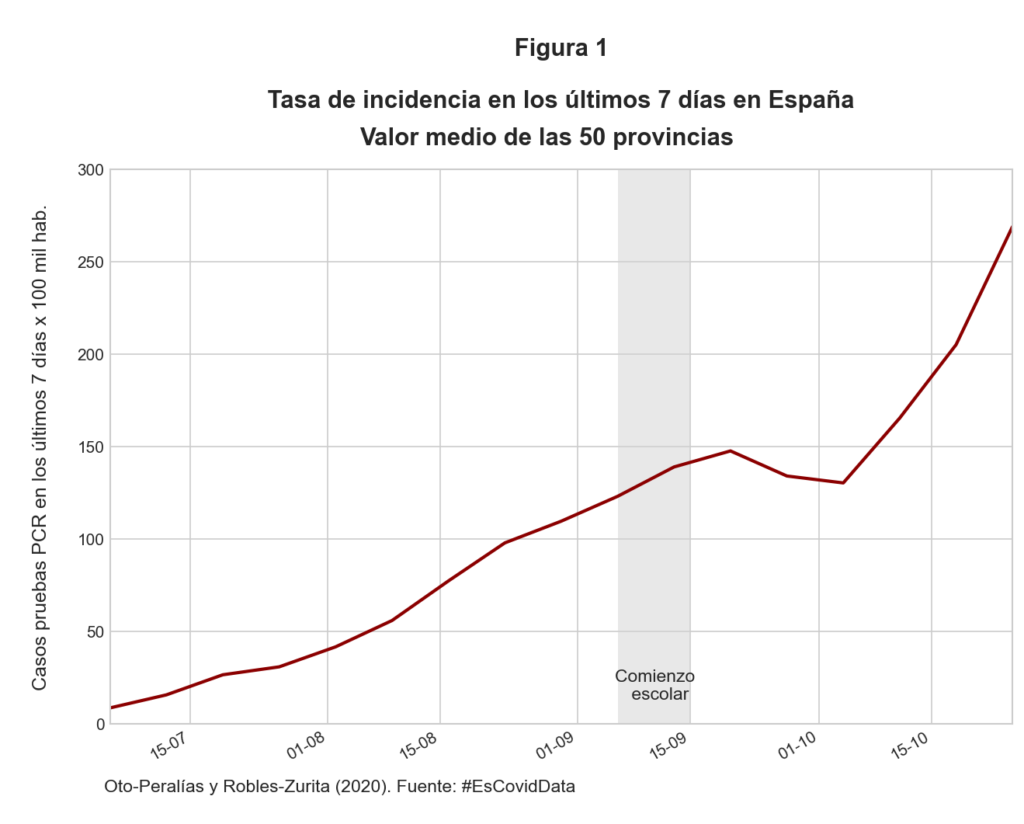
Nosotros examinamos esta cuestión para el caso de España. Una manera sencilla, pero simplista, de analizar el efecto del comienzo escolar consiste en observar cómo han evolucionado los contagios desde entonces. La Figura 1 representa la evolución de la tasa de contagios de los últimos 7 días para la media de las provincias españolas. A la luz del gráfico, no se aprecia una aceleración de los contagios tras la apertura de los colegios. Sí que se observa una aceleración a partir del 5 de octubre, pero el lapso temporal hace dudar que sea atribuible al comienzo escolar. En cualquier caso, este enfoque presenta importantes limitaciones, ya que muchas otras cosas que han tenido lugar durante el periodo de apertura escolar han podido afectar la evolución de la tasa de incidencia.
Nuestra estrategia para medir el efecto de la apertura de los colegios es explotar la variabilidad provincial en el porcentaje de población en edad escolar. La idea subyacente es que el efecto de la apertura, si es que existe, ha debido de ser mayor en las provincias con un porcentaje de población joven más elevado. Así, se puede comparar la evolución de la pandemia entre, por un lado, provincias con un porcentaje elevado de población joven y, por otro, provincias con un porcentaje bajo. La Figura 2 ilustra este enfoque. En ella se clasifican las provincias en 10 deciles según el porcentaje de población menor de 18 años y se muestra la variación desde principios de septiembre de la tasa de incidencia media (en logaritmo). Si la apertura de los colegios ha acelerado la pandemia, deberíamos observar un aumento de la incidencia mayor en los deciles superiores (de color rojo), lo cual no parece que suceda. Por ejemplo, si comparamos los dos deciles superiores (con un porcentaje medio de población joven del 19,4%) con los dos inferiores (13,3 %), la variación entre el 6 de septiembre y el 25 de octubre ha sido 0,67 para el primer grupo, mientras que 0,95 para el segundo. Es decir, los contagios han aumentado más en los municipios con menor porcentaje de población joven.
La Figura 3 es similar a la anterior pero ahora muestra la variación del factor multiplicativo, que es una variable que mide la ratio de la tasa de incidencia con la tasa de la semana anterior. Tampoco parece que la evolución del factor multiplicativo haya divergido sensiblemente desde principios de septiembre.
En el proyecto que estamos desarrollando realizamos este análisis de manera más rigurosa y a varios niveles geográficos. Usamos un modelo de diferencias en diferencias, que en esencia lleva a cabo la comparación anterior. Para fines expositivos, mostramos en la Tabla 1 los resultados de un modelo de regresión de panel donde interaccionamos el porcentaje de población joven con una variable binaria que captura si el periodo es posterior al comienzo de las clases. Este modelo introduce también variables binarias para cada provincia y periodo (es decir, efectos fijos espaciales y temporales). El Panel A emplea las provincias españolas como unidad de observación. Las dos primeras columnas muestran que la evolución de la tasa de incidencia (en niveles y log.) después del comienzo escolar no ha diferido en base al porcentaje de población joven. La tercera columna indica que el factor multiplicativo ha aumentado más (o se ha reducido menos) en las provincias con más población joven (significatividad estadística al 5%). Un examen atento a la Figura 3 sugiere que este efecto de diferencias en diferencias se debe a los elevados factores multiplicativos que las provincias de los deciles inferiores (las de color azul) tenían en el mes de agosto. En todo caso, este resultado no se mantiene cuando cambiamos la unidad de análisis en los paneles B y C.
El Panel B de la Tabla 1 replica este ejercicio para los distritos sanitarios de Andalucía, que son agrupaciones subprovinciales de municipios. Los resultados apuntan a una ausencia de efecto estadísticamente significativo. Por último, en el Panel C descendemos hasta el detalle municipal. Para reducir la heterogeneidad en la muestra, nos centramos en los municipios mayores de 5.000 habitantes, resultando en un total de 257 municipios. Los resultados son consistentes en tanto que no se observa un efecto positivo del comienzo escolar en la evolución de los contagios.
Hemos realizado muchas estimaciones alternativas para las diferentes muestras, usando diferentes intervalos de tiempo, alternaciones en la especificación econométrica, etc. Los resultados casi siempre apuntan a la ausencia de efectos estadísticamente significativos. Aunque los resultados parecen ampliamente consistentes, hay que interpretarlos con la debida cautela. En primer lugar, las provincias (y los municipios) que difieren en el porcentaje de población joven también difieren en otras dimensiones, como su tamaño. Aunque controlamos por todas las características fijas de las provincias (municipios), es posible que, a la par que el comienzo escolar, hayan tenido lugar otras circunstancias que afecten de manera diferente a las provincias (municipios) según su tamaño. No obstante, en estos casos el sesgo probablemente iría en el sentido de una mayor incidencia de contagios, no menor. Es decir, es improbable que oculte un efecto positivo; posiblemente lo amplificaría. En segundo lugar, otra limitación del análisis es que la variabilidad en el porcentaje de población joven no es muy elevada a nivel provincial (ni a nivel municipal cuando excluimos a los municipios pequeños), lo cual puede sesgar a la baja el coeficiente de interés. En relación a esto, aunque no es muy elevada, creemos que la variabilidad es suficiente. Por ejemplo, el porcentaje de población joven del decil provincial 8 es un 28% superior al del decil 2 (18.3/14.3-1). Otra limitación a la que nos enfrentamos es que los datos oficiales de incidencia de la COVID-19 son imperfectos.
Finalmente, cabe destacar la importancia de usar distintos indicadores de la pandemia (tasa de contagios en niveles, tasa en logaritmos y factor multiplicativo) como variables dependientes, como hacemos en nuestro análisis. Limitarnos a una comparación de la tasa de contagios antes y después entre poblaciones con distinto porcentaje de población escolar podría no ser correcto dada la naturaleza de crecimiento exponencial de la pandemia. En ese sentido, pequeñas diferencias interprovinciales en tasa de incidencia antes de la apertura de los colegios podrían convertirse en grandes diferencias con el paso del tiempo; esto ocurriría incluso en ausencia de impacto de la reapertura de los centros educativos. Por ello, el uso de la tasa en logaritmo y el factor multiplicativo de la pandemia sería más apropiado para el periodo de análisis considerado, en el que los casos se han descontrolado debido a un número reproductivo mayor a la unidad.





Hay 6 comentarios
Con este método se plantean dos inconvenientes importantes, 1) no se tiene en cuenta el periodo de incubación de la enfermedad, necesario para entender la transferencia de adultos a menores y viceversa, y 2) se supone que la detección en menores es tan buena como en adultos, cosa que sabemos que no es cierta dada su alta asimptomatologia.
Gracias por tu comentario. Ambas cosas se tienen que tener en cuenta, ¿pero de qué forma?
Respecto al primer punto, lo importante es la definición de antes/después de la apertura. La preparación de los datos es tal que todos los casos producidos tras la apertura de los colegios se codifican en el periodo "después". Por supuesto, de esta forma también estamos incluyendo en "después" casos que en realidad se contagiaron "antes" debido al retraso en la realización de tests (en gran parte dado por el periodo de incubación, pero también por posible saturación del sistema de rastreo, por ejemplo). El problema contrario lo tendríamos si retrasamos la fecha de "antes/después", es decir, muchos casos que en realidad pertenecen al periodo de "después" quedarían registrados en el periodo de "antes". En nuestro análisis, como prueba de robustez, tenemos pensado cambiar la fecha de apertura e incluso eliminar una semana o dos alrededor de la apertura.
Respecto al segundo punto, que la detección sea baja en niños no debería influir mucho porque usamos datos agregados de toda la población. Aunque los niños sean en gran medida asintomáticos, transmiten el virus a grupos de mayor edad, y ello se acabaría reflejando en los datos. Por otra parte, debe tenerse en cuenta que nuestro modelo se basa en cambios en la tasa de contagios a lo largo del tiempo y entre provincias. Además utilizamos variables de cambio relativo (cambios del logaritmo en el tiempo y cambio en el factor multiplicativo). Incluso si la detección es sólo una parte de los infectados reales nuestros modelos calcularían los cambios en las variables correctamente.
Interesantísimo análisis , en esta cuestión del Covid todos los enfoque son necesarios para intentar tener un poco mas de luz y poder tomar mejores decisiones (con base en las mejores evidencias disponibles en vez de al albur de politiqueos).
Un comentario, algunos estudios avanzan que en la poblacion de menos de 18 años el porcentaje de asintomaticos es muchismo mayor, por tanto es posible que haya menos diagnosticados en porcentaje de los casos efectivos. Seria posible que reajustaseis vuestro estudio (de manera directa o mediante proxis)para ver solamente el impacto en los contagiados mayores de 18 años en las diferentes agrupaciones geograficas segun el porcentaje de poblacion menos de 18 años?
Es que sin este ajuste puede que el resultado que habeis obtenido sea casi una profecia autocumplida (como se diagnostican menos casos en los menores de 18 años ya que son asintomaticos en las zonas con mas menores hay menor incidencia).
Gracias por tu comentario, Narciso. Compartimos la opinión de que todos los enfoques son necesarios, de ahí que nos metamos en esto. Sobre el problema del alto porcentaje de asintomáticos entre los niños, te remitimos en parte a la respuesta al comentario de RPOW. En cuanto a lo de "casi una profecia autocumplida", como decimos en dicha respuesta, ten en cuenta que es un análisis relativo, a lo largo del tiempo y entre provincias (o municipios). La idea sobre reajustar el análisis es interesante, pero no hemos encontrado datos provinciales (ni municipales) que muestren la evolución de la tasa de contagios por grupos de edad.
Justamente lo hablaba con mi mujer. Mire está infografia
https://elpais.com/ciencia/2020-10-24/un-salon-un-bar-y-una-clase-asi-contagia-el-coronavirus-en-el-aire.html
Y aplíquela al colegio q por la mañana solo abren la puerta de la clase por el frío... es de cajón soy fan de los análisis y grafos en este caso no son necesarias pero esto como otras cosas pasan de puntillas los periodistas. Si paran los colegios se para la economía así q la consigna periodística es q hay q alarmar pero lo justo.
Los comentarios están cerrados.