Aprendizaje profundo II

La semana pasada describí algunas de las ideas fundamentales detrás del aprendizaje automático. Hoy me toca, como prometí, presentar un brevísimo repaso de las ideas de aprendizaje profundo y su uso de redes neuronales artificiales de múltiples capas.

Neuronas Artificiales

Para ello mi primer cometido es explicar que es una neurona artificial. En la mayoría de los libros de texto, y como uno sospecharía por su propio nombre, las neuronas artificiales y el vocabulario de las mismas se motivan por su analogía con las neuronas naturales existentes en el sistema nervioso de los seres humanos.[1] Y aunque no quiero quitar mérito alguno a tal analogía, que estoy seguro funciona fenomenal con estudiantes provenientes de ingeniería o de ciencias naturales (o dejar de citar a nuestro grandísimo Ramón y Cajal), mi experiencia es que para los estudiantes de economía, quizás como consecuencia de sus menores conocimientos de biología, tal motivación confunde más que ayuda.

Mi explicación habitual cuando enseño a estudiantes de grado en economía enfatiza las neuronas artificiales son una forma de regresión no lineal muy similares a los logits (una idea con la que los economistas ya están familiarizados) y limita, en la medida posible, el uso de vocabulario que sea diferente del que empleamos habitualmente en econometría. Como tales regresiones no lineales, una neurona artificial no es más que una aproximación flexible a una esperanza condicional desconocida.

Más en concreto, una red neuronal es una transformación no lineal de una combinación lineal de variables. Primero, tomamos variables observadas 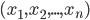y formamos una combinación lineal de los mismas:

\begin{equation*}
z = \sum_{j=1}^{n} \omega_{j}*x_{j}
\end{equation*}

dados unos pesos . La primera variable puede ser una constante y por tanto su peso se llama a veces el sesgo (o intersección en la terminología de regresiones). Segundo, transformamos con una función no-lineal:

\begin{equation*}
y = f(z)
\end{equation*}

Volviendo a mi explicación como esperanza condicional. Un agente se encuentra con el problema de decidir cuál es la esperanza de una variable condicional en unas variables observadas 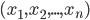o, más concretamente, (que esta relación sea causal o no es irrelevante en este momento; solo estamos buscando un predictor).[2] Sin embargo, esta esperanza condicional es desconocida y la aproximamos como:

\begin{equation*}
y = \mathbb{E}(y|x_{1}, x_{2},...,x_{n}) = f(z) = f\left(\sum_{j=1}^{n} \omega_{j}*x_{j}\right)
\end{equation*}

Esta estrategia funcionará de manera más que satisfactoria en circunstancias normales porque sabemos una función desconocida con ciertas propiedades de regularidad puede ser aproximada arbitrariamente bien con estas regresiones no lineales.

Un ejemplo muy sencillo clarifica la notación y la explicación de la esperanza condicional. Imaginemonos que somos una cadena de supermercados y queremos predecir el número de botellas de mi leche favorita que vamos a vender esta semana en nuestras distintas localizaciones en el area metropolitana de Filadelfia. Podemos seleccionar como variables características demográficas del vecindario (número de habitantes, edad media, renta media, etc.), temporales (temperatura esperada), ventas pasadas, etc. Cada una de estas variables es asignada un peso (volveremos en unos párrafos a cómo tales pesos se determinan, por el momento imaginémonos que un consultor profesional nos los da) y obtenemos un valor . La función transforma ese valor en una predicción de ventas para cada localización.

Llegados a este punto, mis lectores con ciertos conocimientos de economía se estarán preguntado cuál es la novedad de este enfoque con respecto a las regresiones no lineales que llevamos estimando desde hace al menos 60 años. La respuesta es que ninguna. La separación de la no linealidad en mientras mantenemos la estructura lineal en es conveniente, pero no deja de ser un detalle. Lo interesante viene ahora.

Redes Neuronales

Las neuronas artificiales se pueden combinar en diferentes capas para crear redes neuronales. Volviendo a nuestra notación anterior. Nuestras variables se organizan en una primera capa con distintas combinaciones lineales de los mismas:

\begin{equation*}
z_{l}^{(1)} = \sum_{j=1}^{n} \omega_{j,l}^{(1)}*x_{j}, \forall \text{ } l=1,...,L
\end{equation*}

cada una de ellas con pesos . Notemos que ahora los pesos están indiciados tanto por la combinación lineal, en los subíndices 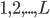, como por la capa, en el superíndice .

Regresando a nuestro ejemplo de predicción de las ventas de botellas de leche en una cadena de supermercados: en vez de construir una sola variable , lo que hemos hecho ahora es construir diferente 's, cada una de las mismas con unos pesos distintos. La variable 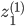puede, imaginémonos, tener pesos más grandes en las variables demográficas y la variable puede preferir, en comparación, ponderar más las variables como ventas pasadas.

Las variables se pueden combinar, a su vez, en una función o emplear como insumos en una segunda capa:

\begin{equation*}
z_{m}^{(2)} = \sum_{j=1}^{L} \omega_{j,m}^{(2)}*z_{j}^{(1)}, \forall \text{ } m=1,...,M
\end{equation*}

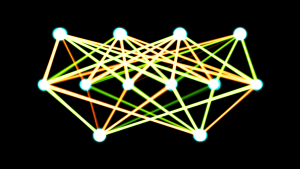
cada una de ellas con pesos . Estas segundas variables son las que se pueden combinar a su vez en una función o servir como insumos en una tercera capa. Es más podemos emplear todas las capas que consideremos necesarias (los libros de texto mencionan que en el cerebro humano las neuronas se organizan hasta en seis capas; carezco de conocimientos para juzgar la exactitud de esta afirmación). Estas capas intermedias se suelen llamar capas ocultas, la capa inicial se suele llamar capa de entrada y la agregación con la función 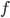, capa de salida. El gráfico que inaugura esta entra es una representación de una red neuronal artificial con una capa de entrada y dos capas ocultas.

Aquí es importante señalar dos puntos. Primero, que el número 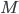de variables en la segunda capa puede ser igual o distinto del número de variables en la primera capa (o en cualquier otra capa). De igual manera podemos cambiar la función 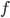en cada capa. Ambas son decisiones del investigador (o quizás del algoritmo, si le damos flexibilidad para ello). Segundo, que esta estructura de capas no es mágica: no hay información nueva alguna diferente de las variables observadas 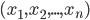. Lo único que hacemos con las distintas capas es crear una ponderación de las mismas altamente no lineal, lo que permite aproximar esperanzas condicionales particularmente complejas, pero en módulos lineales, lo cual es util para su implementación numérica práctica. De hecho, me estoy saltando todos los resultados matemáticos que demuestran relaciones de equivalencia entre distintas estructuras de una red y su posible reducción a una capa única.

Finalmente, y solo por enlazar con las partidas de go que sirvieron como motivación a esta serie, una red neuronal puede ser empleada para evaluar la situación de las fichas en el tablero en un momento determinado de la partida. En el caso del ajedrez, el ordenador sabe donde está cada caballo, torre o peón y, dados unos pesos, encuentra un valor asociado a esta situación. Una vez que tenemos la red neuronal, solo necesitamos que el ordenador encuentre todos los posibles movimientos a partir de la situación actual, compute todas las posibles respuestas del rival (iterando por varios movimientos y eliminando algunas ramas del árbol de movimientos que claramente están dominadas), evaluar el valor asociado a casa situación final después de esos movimientos y seleccionar el movimiento que maximiza tal valor (quizás jugando algún tipo de maxmin). En el caso de go, esta misma estrategia sufre de cuatro problemas. Primero, el tablero es más grande, con lo cual es más complejo capturar su situación con una red neuronal. Segundo, existen muchos más movimientos legales en cada momento (unos 250 en go frente a unos 35 en ajedrez), con lo cual es más difícil computar el valor al final de varias iteraciones. Tercero, al ser todas las fichas iguales (en ajedrez una reina es más valiosa que una torre y tenemos valores convencionales del valor relativo de las fichas que funcionan bien casi siempre), es más intrincado definir unos pesos en la red neuronal que encuentre valores en las posiciones futuras. Cuarto, las partidas suelen durar más (unos 150 movimientos en go frente a unos 80 en ajedrez). Estos cuatro problemas son lo que también empujan a los jugadores humanos de go a emplear la intuición y la imitación de los grandes maestros del pasado más que en ajedrez.

Encontrando pesos

En las dos secciones anteriores he descrito qué es una neurona artificial, cómo se pueden agrupar distintas neuronas en redes neuronales y cómo con estas redes podemos predecir o asignar un valor a una situación en el tablero (o recomendarnos que película queremos ver en Netflix). En toda la discusión, sin embargo, siempre asumí que conocíamos los pesos de la red y que sabíamos qué función emplear.

Ahora me voy a centrar, por tanto, en cómo encontrar estos pesos (las familias de funciones a emplear es más sencilla de explorar, con candidatos naturales como logits). La estrategia más sencilla es estimarlos con datos observados. Obtenemos muchas y muchas 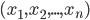y buscamos los pesos que minimizan la distancia (según algún tipo de métrica) entre las observadas y las generadas por la red neuronal. Este problema de minimización es normalmente complejo y es preciso emplear técnicas relativamente sofisticadas, como el gradiente de descenso estocástico, para evitar quedarse atrapado en mínimos locales y encontrar los mínimos globales.[3] De igual manera, y cuando se tienen diferentes capas, hay que ser cuidadoso en como se ajustan los pesos en cada capa (con una propagación hacia atrás; a riesgo de simplificar quizás en exceso y pidiendo disculpas por ello: encontrando derivadas de los errores con respecto a los pesos empleando la regla de la cadena).

Una estrategia que a menudo funciona muy bien, y que yo he empleado en otros contextos, pertenece la familia de algoritmos genéticos:

1) Comenzamos con, por ejemplo, 10.000 valores iniciales de los pesos diferentes generados aleatoriamente. Cada uno de estos 10.000 valores iniciales definen una red neuronal particular.

2) Calculamos entonces cómo de bien cada una de las redes predice los datos. Este paso, en evolución, es la medida de aptitud de una estructura genética a su medio.

3) Seleccionamos, con reemplazo, 10.000 redes neuronales de entre las 10.000 que tenemos según su medida de aptitud. Es decir, las redes que han ajustado los datos mejor tienen una probabilidad más alta de ser seleccionadas y las redes que han ajustado peor una probabilidad más baja. La clave es que esta selección es con reemplazo: la red neuronal 2.345, que ajusta muy bien, puede ser seleccionada cuatro veces mientras que la red neuronal 4.531, que ajusta mal, es seleccionada en cero ocasiones. Como en evolución, las configuraciones genéticas con mayor aptitud tienen una probabilidad más alta de supervivencia y reproducción.

4) Y de igual modo que en la reproducción, ocurrirán mutaciones. Los pesos de la red neuronal 2.345 seleccionada para sobrevivir en el segundo paso del algoritmo no serán los mismos que los de la red 2.345 en la iteración anterior. Introduciremos un pequeño movimiento aleatorio en los mismos. Por ejemplo, si de la red 2.345 en la iteración 1 es 56.98, en la iteración 2 sera 56.98+innovación, donde innovación viene de una distribución Gaussiana (u otra distribución conveniente) con la escala adecuada (hay que encontrar un balance entre mutaciones novedosas y movimiento excesivo de las mismas).

5) Repetimos los pasos 2)-5) varios miles de veces.

6) Al final de la última iteración nos quedamos con la red neuronal que, a lo largo de toda la iteración, se haya ajustado mejor a los datos.

Es importante notar que el algoritmo recoge las dos ideas claves de la evolución: supervivencia (estocástica) de los más adaptados y mutaciones (también estocásticas) que generan nuevas estructuras genéticas. Las mutaciones son las que nos evitan quedarnos en mínimos locales y, bajo ciertas condiciones topológicas de la cadena de Markov implicada por el algoritmo descrito como la recurrencia de Harris en las que no quiero entrar, convergeremos al mínimo global con probabilidad 1. De igual manera, si el lector sabe algo de programación, se habra dado cuenta que este algoritmo son menos de 100 lineas en Julia: es facilísimo de programar y de correr.

En el caso de la predicción de la venta de leche, es obvio como implementar este algoritmo genético. En el caso de las redes neuronales en ajedrez o go, se puede modificar para que las redes jueguen con partidas históricas (en un primer paso), entre ellas (en un segundo paso) o contra seres humanos (en un tercer paso) y en vez de seleccionar las redes que ganan las partidas más a menudo. Esta fue la estrategia de AlphaGo.

Aprendizaje profundo

Finalmente, después de bastante trabajo preliminar, estamos en una situación en la que puedo explicar qué son las técnicas de aprendizaje profundo. Las redes neuronales tradicionales (u otros mecanismos semejantes) tienen un alto grado de estructuración: el diseñador de las mismas decide, basándose en su conocimiento del problema, el número de capas, neuronas, variables observadas, etc. En el ejemplo de la predicción de ventas de leche, el economista tiene que decidir qué variables son relevantes, ponerlas en un formato adecuado (como un fichero con los datos limpios y fáciles de leer por el ordenador), introducirlas en la código, etc. Las técnicas de aprendizaje automático más comunes pueden ayudar en seleccionar las pesos (como describimos antes) o incluso las variables posibles (con un búsqueda voraz como la expuesta la semana pasada), pero al final del día, el ordenador solo puede moverse dentro de un contexto muy estructurado.

Las técnicas de aprendizaje profundo buscan diseñar algoritmos en los cuales podamos dar al ordenador los datos en bruto (por ejemplo, muchos datos demográficos y de venta de leche) y que el ordenador mismo descubra cuáles son los datos relevantes y la estructuración de los mismos, reduciendo así al mínimo los insumos por parte del diseñador humano y facilitando la aplicación del algoritmo a situaciones nuevas y diferentes.

En particular, los algoritmos de aprendizaje profundo emplean cada una de las muchas capas de una red neuronal (o técnicas semejantes) para representar un nivel de abstracción diferente. Una estructura particularmente exitosa de estructurar estas capas múltiples han sido las redes neuronales convolucionales que propusieron Yann LeCun y sus coautores. Estos días las arquitecturas de las redes neuronales convolucionales tienen hasta 20 capas de unidades rectificadoras lineales. Además, estas múltiples capas pueden ser entrenadas con los algoritmos descritos en la sección anterior gracias a la generalización de las GPUs, que permiten la computación masiva en paralelo a un coste muy razonable (aquí un trabajo mío sobre el tema; AlphaGo emplea 280 de estas GPUs).

En el caso de AlphaGo, el programa tiene dos clases diferentes de redes neuronales con múltiples capas. Unas redes, llamadas redes de valor, evalúan la situación en el tablero. Unas segundas redes, llamadas redes de política, evalúan movimientos. Esta división en dos módulos diferentes es particularmente inteligente: en vez de buscar entre todas los posibles movimientos (como se hace en ajedrez, una vez eliminados los movimientos claramente inferiores), la red de política proponen un conjunto razonablemente reducido de movimientos que la red de valor evalúa. La posición el tablero es pasada a unas capas convolucionales como las que mencionábamos anteriormente. Los pesos fueron ajustados, primero mirando a movimientos de seres humanos expertos y posteriormente con ligeramente distintas versiones de las redes jugando entre ellas. Esta estrategia soluciona el problema de cómo evaluar la posición en el tablero de una manera muy diferente que en los programas de ajedrez: estos, por las razones expuestas anteriormente, podían emplear los conocimientos de expertos humanos para definir los pesos necesarios (quizás con ciertas mejoras por simulación). Pero en go no se podía hacer: incluso los mejores expertos tenían problemas en verbalizar porque unas situaciones del tablero eran mejores que otras. Es además el sentido en el que podemos decir que AlphaGo se ha enseñado a si mismo: los pesos no se los ha dado un ser humano, son producto de la evolución del sistema.

Concluyo aquí, ya acercándome a 3.000 palabras y con ello abusando de la paciencia incluso del lector más paciente, mi descripción de las ideas básicas del aprendizaje profundo. Los lectores con más conocimientos sobre estos temas sabrán que me he dejado más cosas en el tintero que las que he podido explicar y que, en varias ocasiones, he simplificado la explicación hasta peligrosamente acercarme a la incorrección. Por ejemplo, no he tenido tiempo de hablar de las redes neuronales recurrentes, que tanto interés han despertado en los tres últimos años. A fin de cuentas el material, para ser desarrollado en detalle, requeriría un libro de texto entero bastante largo (como este en preparación). Pero espero que los lectores con menos conocimientos hayan disfrutado, al menos, de una breve panorámica de las técnicas y las promesas de este campo y que los enlaces les sirvan para profundizar más lejos de mis brevísimas palabras.

1. Como diría Socrates en el Crátilo: περὶ ὀνομάτων ὀρθότητος.

2. Si en vez de la esperanza, buscamos otro momento como un percentil, solo tenemos que definir una función de interés de . Por ello limitarnos a la esperanza condicional no es restrictivo. Si tuviese más espacio, explicaría como podemos movernos de predictores a investigar causalidad. Es suficiente para mi propósito señalar que no hay nada especial en el tratamiento de causalidad en este campo y que aprendemos con las técnicas habituales (como variables instrumentales o experimentos) sigue funcionando aquí con sus fortalezas y debilidades.

3. Sorprendentemente en muchas ocasiones los investigadores han descubierto que distintos mínimos locales producen ajustes que son prácticamente indistinguibles en término de predicción.