 Comienzo este post con una cura de humildad: si en ocasiones anteriores me he burlado de aquellos que no sabían que Turing era el padre de la biología matemática, hoy tengo que confesar, para mi vergüenza, que hasta hace unos días no tenía ni pastelera idea de quién era Evgeni Slutsky (que el pobre no tiene ni entrada de Wikipedia en español). Pido perdón públicamente a todo el mundo de la economía, ya que sus contribuciones al entendimiento de la demanda de los consumidores (de la que casualmente se cumplen cien años este mes) y a los ciclos económicos fueron pioneras y dieron lugar a muchos otros trabajos sobre ambos temas. Pero no se crea, amigo lector, que ha sido ningún economista el que me ha puesto sobre la pista del bueno de Evgeni, no; ¡han sido la Edad Media y el cambio climático!
Comienzo este post con una cura de humildad: si en ocasiones anteriores me he burlado de aquellos que no sabían que Turing era el padre de la biología matemática, hoy tengo que confesar, para mi vergüenza, que hasta hace unos días no tenía ni pastelera idea de quién era Evgeni Slutsky (que el pobre no tiene ni entrada de Wikipedia en español). Pido perdón públicamente a todo el mundo de la economía, ya que sus contribuciones al entendimiento de la demanda de los consumidores (de la que casualmente se cumplen cien años este mes) y a los ciclos económicos fueron pioneras y dieron lugar a muchos otros trabajos sobre ambos temas. Pero no se crea, amigo lector, que ha sido ningún economista el que me ha puesto sobre la pista del bueno de Evgeni, no; ¡han sido la Edad Media y el cambio climático!
Vayamos por partes. Ya sabe usted que el cambio climático es uno de los temas que aparecen recurrentemente en NeG, y yo personalmente como físico que soy lo he tocado en numerosas ocasiones (aquí, aquí, aquí, ...). El caso es que el otro día vi el siguiente tuit:  Y me llamó la atención y me fui a la cita, que no es otra que esta: "The myth of Europe's little ice age" (El mito de la Pequeña Edad del Hielo en Europa). Si va usted al artículo de Wikipedia verá que la Pequeña Edad del Hielo es un período, desde comienzos del siglo XIV hasta mediados del XIX, en el que hizo bastante frío en Europa. Se ha estudiado mucho, tanto en lo que tiene que ver con las posibles causas de esta glaciación en miniatura como con las consecuencias de estar atravesando siglos más fríos de lo normal. Bueno, pues el artículo al que me llevó el tuit, escrito por Morgan Kelly y Cormac Ó Gráda, ambos de University College Dublin, sostiene, refiriéndose a un reciente artículo científico de los mismos autores, que la Pequeña Edad del Hielo no existe.
Y me llamó la atención y me fui a la cita, que no es otra que esta: "The myth of Europe's little ice age" (El mito de la Pequeña Edad del Hielo en Europa). Si va usted al artículo de Wikipedia verá que la Pequeña Edad del Hielo es un período, desde comienzos del siglo XIV hasta mediados del XIX, en el que hizo bastante frío en Europa. Se ha estudiado mucho, tanto en lo que tiene que ver con las posibles causas de esta glaciación en miniatura como con las consecuencias de estar atravesando siglos más fríos de lo normal. Bueno, pues el artículo al que me llevó el tuit, escrito por Morgan Kelly y Cormac Ó Gráda, ambos de University College Dublin, sostiene, refiriéndose a un reciente artículo científico de los mismos autores, que la Pequeña Edad del Hielo no existe.
Así como lo oye: años y años de investigaciones para que al final el objeto investigado no exista. ¿Cómo puede ser eso? Aquí, paciente lector, es donde entra el bueno de Slutsky en nuestra historia. Kelly y Ó Gráda sostienen que el problema con la Pequeña Edad del Hielo es que, para presentar los resultados mejor, se suavizan promediando por bloques de unos cuantos años, es decir, se promedian todas las observaciones desde un instante hasta, por ejemplo, diez más tarde, y así para todos los instantes (lo que en inglés se llama running (o moving) average, y en castellano media móvil). Y resulta que ya en 1927, Slutsky mostró, haciendo un experimento sumando números de lotería, que si uno hace medias móviles de números aleatorios obtiene una serie temporal con oscilaciones aproximadamente periódicas. Aquí está la figura del artículo original de Slutsky (citado en este otro, divulgativo, de la Reserva Federal de Minneapolis),
 y aquí la comparación entre los datos anuales del tiempo en Holanda antes y después de la supuesta pequeña edad del hielo (abajo), y su media móvil (arriba):
y aquí la comparación entre los datos anuales del tiempo en Holanda antes y después de la supuesta pequeña edad del hielo (abajo), y su media móvil (arriba):
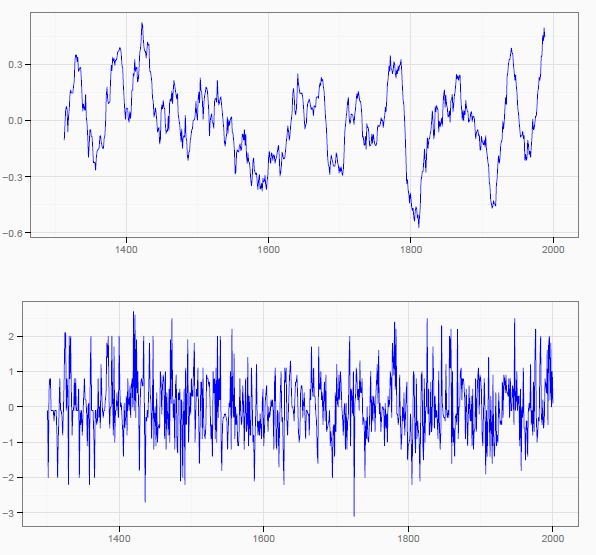 La gráfica superior se obtiene tomando medias móviles de 25 puntos, y parece dar evidencia de esa Pequeña Edad del Hielo: se observa una tendencia decreciente desde la mitad del siglo XV hasta principios del siglo XIX, con episodios más fríos a finales del siglo XVI, del siglo XVII (que se podría conectar con el famoso mínimo de Maunder) y principios del XIX.
La gráfica superior se obtiene tomando medias móviles de 25 puntos, y parece dar evidencia de esa Pequeña Edad del Hielo: se observa una tendencia decreciente desde la mitad del siglo XV hasta principios del siglo XIX, con episodios más fríos a finales del siglo XVI, del siglo XVII (que se podría conectar con el famoso mínimo de Maunder) y principios del XIX.
¿Por qué se llega ahora a esta conclusión? Ajá, tiempo para el tercer actor del post: el cambio climático. Resulta que debido a la preocupación por tener buenos datos para confirmar o desmentir la existencia de un calentamiento global, se ha mejorado mucho la reconstrucción histórica de las temperaturas en varias regiones de Europa. Incluso, en algún caso, se han comparado con datos económicos para comprobar cómo de buenas eran esas reconstrucciones: es el caso de los Países Bajos, por ejemplo, para los que la evolución temporal de la temperatura encaja muy bien con la variación de precios del trigo en los siglos del XIII al XVI. Así, utilizando esos datos mejorados, y teniendo en cuenta el efecto Slutsky tal y como le llaman Kelly y Ó Gráda (cuyo artículo, amigo lector, le recomiendo vivamente si lee usted inglés), parece deducirse que la Pequeña Edad del Hielo Europea tiene muy poco apoyo estadístico. Ojo, amigo lector, que en ciencia nunca nada es totalmente definitivo: "poco apoyo estadístico" quiere decir eso, que es poco probable que ocurriera, pero no que esté totalmente descartada. Con todo y eso, es un contratiempo bastante serio para un sector amplio de historiadores que busca explicar los avatares de nuestro pasado a través de las circunstancias climatológicas, y habla de la necesidad de disponer de evidencias muy sólidas para trabajar en esa dirección. Un buen ejemplo es el estudio de la relación de la sequía con el colapso de la civilización maya del que hablé en este post, en el que los investigadores utilizan evidencia geológica de la pluviosidad anual.
Pero claro, una cosa lleva a la otra, y después de enterarme de que igual hay que reescribir muchas cosas de la historia medieval, me quedé muy intrigado sobre Slutsky. Y así es cómo aprendí que este caballero era un matemático, un estadístico, ruso, que tenía gran interés en aplicar las matemáticas a la economía. Por eso se planteó su experimento de las sumas de números aleatorios: porque estaba interesado en entender el origen de los ciclos económicos, como muchos otros economistas de su época (y de la nuestra). A partir de aquí pido a mis amigos de NeG y demás economistas perdón por anticipado por las burradas que pueda decir, así como ayuda para corregirlas en los comentarios. Así prevenidos, vamos a ello: las economías, representadas por las magnitudes macroeconómicas, tienen períodos de bonanza o de ascenso seguidos por otros peores o de decrecimiento, que se suceden de manera más o menos periódica. La existencia de estos ciclos, conocida desde hace al menos doscientos años, intrigó a buena parte de los economistas, que propusieron todo tipo de teorías para explicar su existencia, incluida la influencia de las manchas solares (explorada por el economista del siglo XIX William S. Jevons; desde entonces se habla de equilibrios de manchas solares a las teorías que invocan influencias exógenas en la evolución de la economía).
Slutsky se planteó el problema de los números aleatorios para comprobar si era posible que los ciclos económicos obedecieran, en vez de a esas influencias exógenas periódicas, a sucesos o shocks aleatorios de diferentes tipos y sin periodicidad alguna (catástrofes naturales, malas cosechas, guerras, etc.). Por eso se puso a hacer medias móviles de los dígitos de números de lotería, y obtuvo la gráfica que aparece más arriba, donde incluye como comparación en la línea de puntos un índice de la economía británica. Obviamente, el parecido es totalmente casual, pero la gráfica sí sugiere que una explicación en términos de esos sucesos aleatorios podría estar detrás de las observaciones macroeconómicas. El trabajo de Slutsky abrió la puerta a explorar esta opción, y dado que no tengo tiempo para entrar en ello aquí, recomiendo por ejemplo el trabajo que he citado antes de Davies y Mahon. En cuanto a Slutsky, al poco de publicar su trabajo [que apareció ampliado en Econometrica diez años después: "The Summation of Random Causes as the Source of Cyclic Processes (1937)"] dejó la investigación en economía, fundamentalmente por miedo a Stalin, que había encarcelado (y posteriormente fusilado) a su jefe Kondratiev por su oposición a sus medidas económicas (como las colectivizaciones).
No me resisto a decir unas palabras sobre el mecanismo que hay detrás de la aparición de estas oscilaciones en las sumas de números aleatorios. La clave está en observar que cada número entra en tantas medias móviles como números promediamos para hacerlas. Supongamos por ejemplo que mis números aleatorios son 59284517392641716282859272752 (que acabo de generar tecleando y que es todo menos aleatoria, porque por ejemplo nunca se repite un número en posiciones consecutivas), y que hacemos medias móviles sobre 10 números. El resultado es 5.3, 5.0, 4.7, 4.9, 4.2, ... etc., que como se ve parece tener una tendencia a bajar. Esa tendencia solo refleja la desaparición de las medias móviles del 9 y el 8 que aparecen en segundo y cuarto puesto, respectivamente, y su sustitución por números más pequeños; a medida que progresemos en la serie, se producirá el fenómeno contrario y detectaremos tendencias ascendentes. De hecho Slutsky llegó a probar que si la serie fuera infinita y el tamaño de la media móvil suficientemente grande, ¡obtendríamos una función sinusoidal perfecta!
¿Y todo esto, salvo la corrección de la idea de la Pequeña Edad de Hielo, qué tiene que ver con el cambio climático, mi tercer actor del post? Pues mucho, y hay que ser muy cuidadoso con esto. Ahora seguro que alguno aprovecha para decir, "¿veis?, ya os decía yo que el calentamiento global es una chorrada producto de errores estadísticos." Pues va a ser que no. En primer lugar, no es un problema tipo efecto Slutsky porque el efecto Slutsky causa oscilaciones en torno a una media constante, y aquí observamos que la temperatura sube. Podría ser otro artefacto estadístico, pero no ese. Pero en segundo lugar, y lo más importante, es que precisamente por su importancia, como dije más arriba, las series temporales de temperaturas y su tratamiento estadístico están siendo revisados y mejorados continuamente. En este sentido, me parece lo más apropiado terminar este post con una mala noticia para los "negacionistas": acaba de aparecer un trabajo en Science, "Possible artifacts of data biases in the recent global surface warming hiatus", que reanaliza los datos que parecían indicar que el aumento de la temperatura se había detenido en los últimos años (a esto es a lo que se venía llamando "surface warming hiatus"). Como se puede ver en la gráfica,
las tasas de crecimiento de la temperatura en distintos períodos y o bien globales o bien del océano y de los continentes se vuelven significativamente positivas al reanalizarlas (cuadrados, en la figura). El cambio en los resultados se debe, de manera muy resumida, a avances en tres direcciones: la comparación de resultados de boyas y barcos en la superficie marina, que discrepan sistemáticamente, de la que se ha podido confirmar que los datos de las boyas son más fiables; a diferencias en las tomas de datos por barcos antes y después de la Segunda Guerra Mundial, que no estaban bien tenidas en cuenta; y a una mejora en los registros históricos y su integración, que en este estudio cuentan con el doble de fuentes. Total, que al final ese argumento que venían utilizando los negacionistas para objetar a la existencia del cambio climático, el supuesto parón en el aumento de la temperatura, es tan poco probable como la Pequeña Edad de Hielo. Agradezcamos a los Slutskys de ayer y de hoy su esfuerzo en comprobar y mejorar los análisis estadísticos para tener cada vez más certeza (que nunca seguridad absoluta) de que al menos sabemos qué está pasando, aunque no lo entendamos, como en el caso de los ciclos económicos, que no en el calentamiento global.
 Y le recuerdo, amigo lector, el calentamiento global existe, pero el que llevemos un mes o más cociéndonos en nuestro propio jugo no lo demuestra, como ya le dije en otro post (véase también este artículo). Lo que sí parece verdad, sin embargo, es que vamos camino de un nuevo record de temperatura en 2015. Y los gobiernos mundiales, a verlas venir (por no hablar de otros que se dedican a sabotear las energías renovables con saña y entusiasmo). A ver si la cumbre de París de finales de año sirve para algo. Me temo que no soy optimista...
Y le recuerdo, amigo lector, el calentamiento global existe, pero el que llevemos un mes o más cociéndonos en nuestro propio jugo no lo demuestra, como ya le dije en otro post (véase también este artículo). Lo que sí parece verdad, sin embargo, es que vamos camino de un nuevo record de temperatura en 2015. Y los gobiernos mundiales, a verlas venir (por no hablar de otros que se dedican a sabotear las energías renovables con saña y entusiasmo). A ver si la cumbre de París de finales de año sirve para algo. Me temo que no soy optimista...


Hay 20 comentarios
No entiendo muy bien porque en esto del cambio climatico abunda el lenguaje sectario mas propio de otros ambitos que de la ciencia.
Entre los principales defensores de las Teorias del Cambio Climatico han abundado las exageraciones, el catastrofismo y hasta la manipulacion. Recordemos el infame documental de Al Gore...
Eso ha causado rechazo en muchos cientificos y personas criticas y dudas legitimas. No del fenomeno en si, sino de la fiabilidad de las predicciones, de los efectos reales de la subida de las temperaturas y de los intereses creados por la tupida red de subvenciones a la industria del Cambio Climatico, y de si lo mejor es no hacer mucho caso de los informes habituales.
El lenguaje de fan de futbol y la calificacion de los discrepantes de "negacionistas " creo que deberia eliminarse de esta rama de la ciencia. No aporta nada al argumento cientifico.
Personalmente no me creo las predicciones, ni creo fueran tan dañinas si ocurrieran. Los modelos climaticos me causan muchas dudas. Al parecer los Dinosaurios vivieron felices con altisimos niveles de carbono. Nosotros que somos mas listos igual tambien podriamos.
Fernando, el lenguaje sectario es el apropiado para tratar con sectas. Hay dos clases de personas: los que aceptan (críticamente) la evidencia científica, y los que no. Estos últimos, como personas acientíficas, son una religión o una secta, que tanto me da. Y por tanto llamarlos "negacionistas" no es más que referirse a lo que hacen, negar sectariamente la evidencia. Los negacionistas son precisamente los que no aportan nada al debate científico porque no usan argumentos científicos, que se pueden rebatir o incluso adoptar si se demuestran ciertos. "No me creo las predicciones" es un argumento perfectamente legítimo, pero lo que no es es científico en vista de la evidencia de la que actualmente se dispone, que acepta una gran mayoría de científicos. La verdad es que ya me aburre un poco tener que discutir esto. Así que sí, cada uno es libre de creer lo que le da gana, como que el cambio climático no existe o no es causado por el hombre, o incluso que la homeopatía cura el cáncer de páncreas, pero que no pretenda entrar en debates científicos.
No me extraña que esté usted aburrido de discutir estas cosas. Por si sirve: tomando como pretexto las declaraciones de un negacionista redomado me he permitido hacer esta síntesis de los fundamentos que evidencian el calentamiento global y la seriedad del riesgo del cambio climático (y no hace falta recurrir a las predicciones de ningún modelo):
http://lasendadelcrecimiento.blogspot.com.es/2015/07/naciones-unidas-el-clima-y-las-teorias.html
Por otra parte, yo tampoco tenía ni "pastelera" idea de quién era Slutsky ni de su trabajo, y creo que me va a resultar muy interesante conocerlo. ¡Muchas gracias!
Nadie duda que el efecto inverdadero existe, y que las emisiones industriales son causantes de los niveles en la atmosfera. Pero la prediccion del clima es algo mucho mas complejo. Para empezar de momento es imposible predecir con alguna fiabilidad el efecto de las nubes que actua en sentido inverso y estabiliza el clima. Tampoco se conoce muy bien el factor de estabilizacion de los oceanos. Y el efectodel Niño aparente conocido nos sigue sorprendiendo.
No esta claramente explicado como se produce el fenomeno periodico de las glaciaciones. Que en principio parecen mucho mas peligrosas.
Tampoco se sabe muy bien por que la temperatura actual de la Tierra es la optima y no dos grados mas o dos grados menos. Nadie lo ha explicado. No esta claro si el enfriamiento es peor o mejor que el calentamiento. Muchos piensan que es mucho peor el enfriamiento.
Tampoco esta bien explicado por que en el Pleistoceno altisimos niveles de carbono convivian con una vitalidad en animales y vegetales muy superior a la actual.
Por otra parte parece obvio que el calentamiento puede empeorar las condiciones climaticas en algunos sitios y mejorarlos en otros. Decir que empeora en todos los sitios va contra la logica y hace la teoria poco creible.
No parece logico que se preocupen del calentamiento global en Rusia ni en Suecia. Tampoco en Arabia. Entre estar de media a 40 o 43 tampoco hay tanta diferencia.
Anxo,
Las predicciones, son predicciones, y no se tiene evidencia cientifica de una teoria o modelo de prediccion hasta que experimentalmente se demuestra por el exito sistematico de sus resultados.
Hasta ahora que yo sepa , no hay un modelo matematico de clima que haya demostrado experimentalmente su exactitud. Si lo conoce le ruego me de algun enlace donde pueda verlo. Me refiero al exito de sus resultados en sus predicciones. No a como esta construido, ni las razones por las que debe funcionar.
El metodo cientifico se basa en la comprobacion de las teorias por la experimentacion. Al menos es lo que yo aprendi en la universidad.
Por favor faciliteme la evidencia del experimento positivo de los modelos matematicos de prediccion o acepte cierto escepticismo cientifico. No me vale el criterio de Autoridad. Ya no estamos en la Edad Media.
Lo de no usar un lenguaje sectario solo era una sugerencia. Si no esta de acuerdo no tiene mayor importancia.
Fernando, hay no uno sino muchos modelos que están bastante de acuerdo con el comportamiento observado de la temperatura. Lo que ocurre es que tienen (como todo) su margen de error y eso hace que estemos seguros al 100% de que aciertan, o de cuáles aciertan. Por eso se habla de consenso entre los científicos. En cualquier caso en la página web del IPCC, como referencia fundamental, tienes todos los datos en los que la comunidad científica se basa para afirmar que el cambio climático existe y que lo causamos nosotros. En tu otro comentario hablas de que puede no importar dos grados arriba o abajo, de nuevo te recomiendo que leas los informes del IPCC para que veas si importa o no.
https://es.wikipedia.org/wiki/Yevgeni_Slutski (!?)
Gracias! No la había encontrado, no sé por qué.
¡A mí no me pregunte! 😀
Como hipótesis: si empezó directamente en la Wikipedia en español probablemente sea un problema derivado de la romanización del alfabeto cirílico (https://es.wikipedia.org/wiki/Romanizaci%C3%B3n_del_ruso), por experiencia personal le puedo asegurar que es bastante lioso.
Si comenzó por la Wikipedia en inglés, una ceguera momentánea... (si no se repite no creo que sea muy preocupante, pero no soy médico)
Por otra parte, un post muy interesante. En mi caso estaba familiarizado con el Slutzky estadístico y su trabajo en Economía, pero no tenía ni idea de alguna de las facetas que Vd. menciona.
¡Buen verano!
El articulo enlazado sobre el efecto Slutsky de la pagina de la Fed de Minneapolis y su relacion con la teoria macroeconomica de los ciclos es oro puro. Muchas gracias!
Gracias a ti por leerme, peter.
Curioso. Conocía el "Slutsky económico" (por micro de 2º), pero no el "matemático" y su relación con Kondratiev.
Muy interesante la aportación.
Gracias Estilpon, yo no conocía a ninguno! Por eso esta entrada la he disfrutado yo mismo más que otras...
Un post muy interesante, aunque yo haría varias observaciones:
1-Creo que queda un poco confuso en el artículo la diferenciación entre ciclos y tendencia. Que haya ciclos provocados por esa aleatoriedad no significa que no pueda haber una tendencia. De hecho, muchas veces van juntos los ciclos y la tendencia ¿Dónde estaría la humanidad si a los ciclos económicos no le acompañara una tendencia? Tendencia a mejorar, claro.
2-Si se utilizan medias móviles es para eliminar el ruido que implica utilizar las observaciones individuales. El gráfico de medias móviles de la temperatura en Holanda ayuda a visualizar una tendencia descendente, además de los posibles ciclos, entre inicios de 1400 y 1600. En el resto no se aprecia dicha tendencia. Como es lógico, en el gráfico de datos individuales no se ve nada ya que hay mucho ruido, aunque habría que analizarlo... ya se sabe que los gráficos son como las nubes, cuanto más los miras más formas acabas viendo.
Por tanto, no acabo de ver la demostración de que no existiera la pequeña edad de hielo…
Gracias Jordi. Es muy cierto lo que dices de las tendencias. Lo que cuento de Slutsky se refiere a series temporales sin tendencia o si quieres de media cero, si bien hay resultados equivalentes aunque más complicados matemáticamente para el caso con tendencia. En cuanto a tu segunda observación, el problema es que el promediado te da cosas que no son las quue se observan, y aunque haya una cierta tendencia descendente en el período que dices (pero que como también dices habría que estudiar con bastante más cuidado, y que de hecho yo no veo más que en el tramo final), no hay un período continuado de bajas temperaturas como el que se atribuía a la Pequeña Edad de Hielo, que es de lo que se trata. Fíjate además en la diferencia de escalas: las fluctuaciones anuales están medidas en grados y la gráfica de medias móviles en décimas de grado, es decir, que cualquier posible tendencia es bastante irrelevante comparada con la variación anual. En todo caso la gráfica es un ejemplo y el post un resumen muy superficial del tema, y si quieres verlo en profundidad te remito al artículo original que lo contarán mejor que yo. Gracias por leerme y por molestarte en transmitir tus observaciones!
Desde el punto de vista puramente matemático, el teorema de Slutsky establece en su primera proposición:
Sean {Xn}, {Yn} sucesiones de variables aleatorias.
Es decir, para que fuera de aplicación al estudio del clima, primero habría que demostrar que el clima, al menos en la pequeña edad del hielo, sigue un comportamiento puramente aleatorio. Lo cual, por cierto, invalidaría tanto la pequeña edad del hielo, como el cambio climático actual. Luego, según entiendo yo, no está claro que el teorema de Slutsky sea de aplicación aquí, o que, al menos, pueda usarse para negar la pequeña edad del hielo sin implicar la negación simultánea del cambio climático actual, ¿no cree?
Gracias Antonio. En primer lugar, como ya he dicho antes respondiendo a Jordi, lo que dices es cierto, y el teorema de Slutsky no vale tal cual, pero hay versiones para esos casos. Y en segundo lugar, como también le dije a Jordi, el artículo que ataca la idea de la Pequeña Edad de Hielo usas bastantes más evidencias, que puedes leer, no sólo se basa en Slutsky. Hay que entender que en un post como este, que se pretende que sea inteligible y que tenga 1500 palabras (como me dice siempre Sam Bentolila con buen criterio, pero que siempre me paso) no se puede explicar todo ni con todo rigor. Pero ahí están las fuentes para el interesado en los detalles.
Fabuloso post, por lo que aporta y por la humildad y buen humor del aportante. Con este tono no importa que sean más de 1.500. Saludos,
Gracias Pedro Luis, me alegra que te haya gustado. A lo de la humildad no te acostumbres que me cuesta mucho...
Gracias por el post.
Permíteme una pequeña puntualización:
"De hecho Slutsky llegó a probar que si la serie fuera infinita y el tamaño de la media móvil suficientemente grande, ¡obtendríamos una función sinusoidal perfecta!"
Si no entiendo mal el paper de Slutsky, esto, referido a una media móbil de números aleatorios independientes, no es cierto, ya que no cumple las codiciones del teorema A.
Él lo prueba para una serie donde cada término es la m-diferencia de la n-suma de una serie de números independientes (Teorema B).
Los comentarios están cerrados.