Esta entrada es conjunta con Federico Pablo-Martí.
 En Nada es Gratis se discute con mucha frecuencia el tema del transporte, como factor económico de primera magnitud, tanto en sí mismo como por lo que tiene de facilitador para muchos otros sectores (como en esta o esta entradas de Gerard, o esta otra). Hoy queremos aportar una perspectiva algo más abstracta sobre el problema, basada en este trabajo que hemos publicado recientemente sobre las consecuencias que tienen las decisiones y criterios políticos sobre la evolución de las redes de transporte. Cuando acabe usted de leer, amigo lector, esperamos haberle convencido de que la evolución de una red de transporte depende mucho del criterio con el que se vayan seleccionando los tramos sobre los que actuar; para ello, le daremos algunos ejemplos de criterios y veremos qué resultados arrojan. Por tanto, la valoración de una política de infraestructuras solo se puede hacer en base a los criterios que llevaron a su diseño; además, como también veremos, no se puede tratar aisladamente distintas conexiones de transporte sin tener en cuenta su efecto sobre toda la red. Para terminar, trasladaremos las consecuencias de nuestras elucubraciones teóricas a políticas de transporte presentes y pasadas. Vamos a ello, pues.
En Nada es Gratis se discute con mucha frecuencia el tema del transporte, como factor económico de primera magnitud, tanto en sí mismo como por lo que tiene de facilitador para muchos otros sectores (como en esta o esta entradas de Gerard, o esta otra). Hoy queremos aportar una perspectiva algo más abstracta sobre el problema, basada en este trabajo que hemos publicado recientemente sobre las consecuencias que tienen las decisiones y criterios políticos sobre la evolución de las redes de transporte. Cuando acabe usted de leer, amigo lector, esperamos haberle convencido de que la evolución de una red de transporte depende mucho del criterio con el que se vayan seleccionando los tramos sobre los que actuar; para ello, le daremos algunos ejemplos de criterios y veremos qué resultados arrojan. Por tanto, la valoración de una política de infraestructuras solo se puede hacer en base a los criterios que llevaron a su diseño; además, como también veremos, no se puede tratar aisladamente distintas conexiones de transporte sin tener en cuenta su efecto sobre toda la red. Para terminar, trasladaremos las consecuencias de nuestras elucubraciones teóricas a políticas de transporte presentes y pasadas. Vamos a ello, pues.
Lo que nosotros hemos hecho es intentar estudiar qué ocurre cuando sobre la red de transporte sigue un proceso "histórico", es decir, cuando no nos planteamos el problema desde el principio sino que la red crece y se va mejorando en una secuencia temporal, y donde las decisiones sobre qué tramos se deben construir o mejorar se toman con distintos criterios. Es importante entender esto, porque lo que no estamos haciendo es una optimización, un diseño centralizado de la red que mejor verifique unos criterios y que se construye de una vez por todas. En realidad, si lo piensa, querido lector, así es cómo realmente ocurren las cosas, y en ningún sitio se ha diseñado la red de transporte como resultado de una optimización (otro contexto donde esto es evidente, más allá de las ciudades, es el del desarrollo de las líneas de metro en cualquier gran ciudad). Por tanto, nosotros partimos de que hay una red que existe en un momento dado, y sobre esa red se van ejecutando mejoras de distintos tramos. En nuestro trabajo hemos considerado dos tipos de redes preexistentes: la red completa, en la que se puede ir directamente de cualquier sitio a cualquier otro (que podría describir un estudio sobre transporte aéreo, por ejemplo), y la red de Delaunay, un tipo de red que conecta cada ciudad con sus vecinas de manera eficiente, que es lo más realista desde el punto de vista del transporte terrestre.
Vayamos ahora con la geografía, para concretar qué pasa en distintas situaciones tipo dependiendo de como estén distribuidas las conexiones que queremos mejorar. En nuestro trabajo, consideramos distintos "países", donde las "ciudades" están distribuidas de distinta manera. La figura que aparece a continuación recoge cuatro de estos "países" tipo muy diferentes:
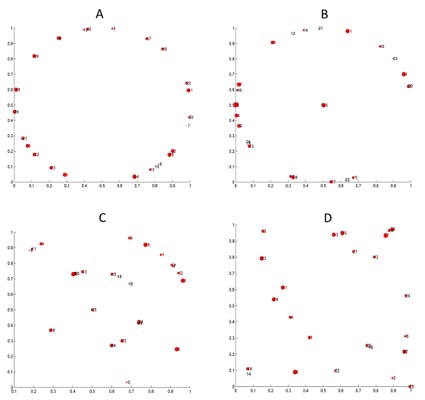
El país A tiene sus ciudades distribuidas exclusivamente en la periferia, como puede ser el caso de Islandia o de Escocia; países con un interior muy accidentado y/o inhóspito. El B y el C tienen además una ciudad central, a la que en el país C se añade una doble circunferencia de ciudades. Estas pueden ser abstracciones similares a Francia o España. Por último, en el país D las ciudades están dispuestas al azar, sin orden alguno; compárese con el caso de Alemania, donde sus ciudades surgen de una historia de pequeños reinos que se han integrado hace relativamente poco.
Aquí viene lo importante: ¿con qué criterio vamos a escoger los tramos que vamos a abordar sucesivamente? Esta, como veremos, es la clave de la cuestión, ya que distintos criterios conducen a distintas redes. Nosotros hemos estudiado tres criterios, pero pueden analizarse muchos otros. Los que nosotros consideramos fueron:
- Accesibilidad. Cada ciudad tiene un "voto" sobre qué tramo se va a mejorar. En nuestro modelo, las ciudades votan para intentar reducir el tiempo total de los viajes entre todas ellas (fíjese en que esto es un modelo que se simula por ordenador, y por tanto tenemos que simular cómo toma su decisión cada ciudad, en este y en cualquier otro criterio).
- Accesibilidad ponderada por población. Cada ciudad tiene un "voto" pero ese voto está pesado por la población, y las ciudades lo que quieren es reducir el coste total de los viajes para la población.
- Tráfico ponderado por población. Cada ciudad tiene un "voto", de nuevo pesado por la población, pero ahora para intentar incrementar el tráfico. En el modelo se asigna a cada tramo un tráfico proporcional a la población de las ciudades unidas por ese tramo e inversamente proporcional al cuadrado de la distancia que los separa (modelo gravitacional).
¿Qué es lo que ocurre en cada caso? Las figuras a continuación presentan ejemplos de lo que ocurre cuando se mejoran las conexiones entre las ciudades que estamos considerando (más ejemplos aquí). Se representa el estado tras mejorar 15 tramos. Cada fila corresponde a un tipo de ciudad, y cada columna a un criterio. La gráfica muestra de manera muy clara que, para cada geografía, la red que emerge del proceso de mejoras depende del criterio con el que se eligen los tramos.
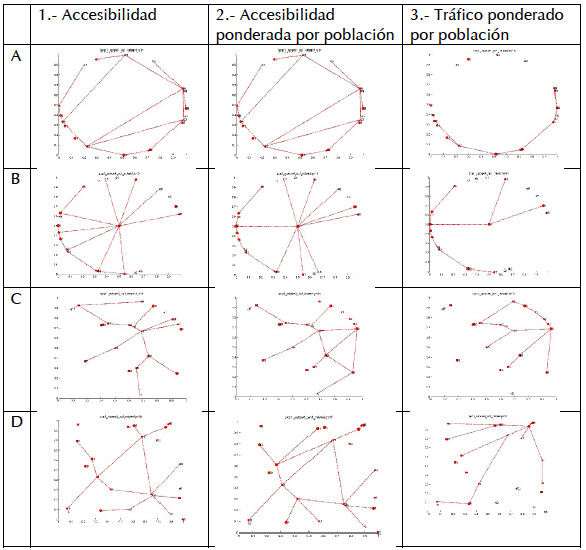
Por otro lado, es particularmente interesante lo que ocurre durante la evolución del proceso. Para ello nos fijamos en la centralidad, que es el concepto que se usa al tratar de redes complejas (véase también esta o esta entradas) para ver cómo de importante es un nodo, en este caso, una ciudad. Hay muchas maneras de medir la centralidad, pero nosotros nos vamos a fijar sólo en dos: la centralidad de grado, que asigna mayor importancia a un nodo cuántas más conexiones directas tiene, y la centralidad "betweenness", para la que la importancia tiene que ver con la aparición de un nodo en más caminos más cortos entre otros. La figura siguiente recoge, por poner un ejemplo, cómo van cambiando las centralidades en el caso de país desordenado (Alemania), con decisiones que se toman con los tres criterios. Aquí es importante aclarar que cada punto corresponde al coeficiente de Gini total de la distribución de centralidades, que nos mide cuánto de desigual es la distribución de centralidad entre las distintas ciudades. Un coeficiente de Gini más cercano a 1 es una distribución muy desigual, mientras que 0 corresponde a la situación en la que todas las ciudades son igual de importantes.
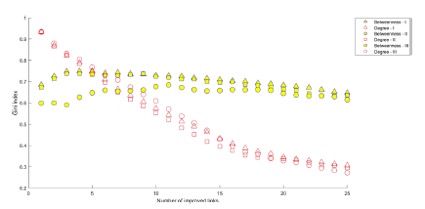
En el gráfico se aprecia que la centralidad de grado ("degree") varía mucho durante el proceso, lo cuál es lógico: al mejorar el primer tramo solo hay dos ciudades realmente centrales, el resto siguen sufriendo una red antigua. A medida que se mejoran tramos adicionales, más ciudades se van incorporando al club de las bien tratadas. Sin embargo, la centralidad "betweenness" no varía gran cosa, y de hecho tiene un comportamiento peculiar al principio del proceso dependiendo del criterio, con aumentos de la desigualdad entre ciudades al avanzar la mejora de la red. Pero además de las características globales, numéricas, conviene observar que aunque las redes finales pudieran ser muy parecidas en algunos casos, el proceso histórico es totalmente distinto, por lo que si se detiene antes de haber conectado todas las ciudades (por ejemplo por una crisis económica o por agotamiento del presupuesto) el resultado puede ser muy diferente.
Como vemos, hay bastantes lecciones que podemos extraer de este trabajo puramente teórico: para empezar, como ya adelantamos, aunque las mejoras sean locales, hay que ver la red como un todo. Los cambios de centralidad y la desigualdad que inducen son muy relevantes, y pueden dar durante un tiempo una ventaja competitiva a ciertas ciudades o nodos. Esto debe valorarse tanto en términos de consecuencias de las decisiones tomadas como una posible medida a adoptar para promocionar ciertos nodos. Pero sólo puede valorarse con el dato de toda la red. En segundo lugar, la valoración de una política de infraestructuras sólo se puede hacer en base a los criterios escogidos. Se podría encontrar una combinación de objetivos para los que la red evaluada sería óptima, y al revés, ninguna red puede ser óptima para la totalidad de objetivos. Por tanto, es imprescindible determinar el marco de referencia y su relación con el mandato político subyacente. Por ejemplo, si al agente decisor se le pide una red que maximice algo para el conjunto de agentes no puede pedírsele que sea óptima simultáneamente para un subconjunto: Que el corredor ferroviario mediterráneo se haya pospuesto puede ser potencialmente razonable desde una perspectiva nacional pero profundamente ineficiente para las comunidades afectadas. Como consecuencia, resulta de crucial importancia determinar los objetivos y los agentes decisores relevantes en cada proceso de inversión. Y, por supuesto, los políticos deben ayudar a la ciudadanía mostrando las repercusiones reales de las inversiones y no solo las aparentes (una ciudad puede tener muchas conexiones (grado) y sin embargo casi ningún viajero la atraviesa ("betweenness").
Una reflexión adicional sobre este tema nos lleva a hablar de los criterios de eficiencia y equidad, que probablemente sean bastantes contrarios cuando se trata de infraestructuras. Si queremos incentivar las zonas más atrasadas o despobladas probablemente supondrá un coste en términos de crecimiento para el sistema global. Dado que las ventajas de las zonas centrales son muy altas respecto a las deprimidas conseguir su expansión podría requerir de inversiones muy altas o incluso no ser posible. Ejemplo: Zamora podría no ser atractiva a las empresas aunque el número de carriles de sus autopistas continúe creciendo indefinidamente. Solamente un empeoramiento en las autopistas de Madrid con el consiguiente aumento de la congestión podría hacerlo. Esto apunta a que probablemente sea necesario otro tipo de intervenciones y, claro, a que las decisiones sobre las redes de transporte son de una complejidad extraordinaria, que no conviene abordar a la ligera ni como moneda de cambio en negociaciones políticas, sin base científica y técnica de ninguna especie.
Para terminar, no nos resistimos a hacer un último comentario sobre otra posible utilidad de este tipo de estudios, de carácter más básico, en el ámbito del análisis histórico. La generación de redes artificiales a partir de la combinación de datos históricos con hipótesis sobre los criterios de selección de inversiones que fueron aplicados permite la generación de redes contrafactuales. La comparación de las redes artificiales con la red empírica permite contrastar la validez de las hipótesis planteadas en su elaboración. Un ejemplo de ello puede verse en el documento de trabajo realizado por Myro et al (2014) en el que se indaga sobre las motivaciones del diseño radial de la red de carreteras españolas que evoluciona a partir de la elección en el siglo XVI de Madrid como capital. Así pues, el tipo de trabajo que acabamos de resumir puede ser muy útil en un aspecto más "forense", de análisis de las razones que llevaron al estado de la red en el momento de interés.