La utilización del sistema de videoarbitraje (VAR) para revisar decisiones arbitrales controvertidas ha desatado muchos debates y discusiones de café. La controversia a menudo giran sobre si este sistema beneficia a los equipos grandes, si generan demasiadas interrupciones y, en definitiva, si hemos ganado algo con su implantación. Una clara mejora que se destaca es que, en principio, deberían cometerse menos errores arbitrales. Otra posible mejora, tal vez menos obvia, es que el VAR podría hacer que, en equilibrio, los jugadores comentieran menos infracciones. Esto es lo que predice el modelo de crimen (ver aquí) de Gary Becker que ya discutí en otra entrada, aunque con un objetivo diferente (ver aquí). La idea de esta entrada es tratar a un jugador que hace algo ilegal como un “criminal”: al fin y al cabo, excepto en casos no intencionados, cometer una infracción en el campo consiste en saltarse las reglas establecidas con el objetivo de obtener algún beneficio con ello. Así pues, en lo que sigue me refiero a futbolistas criminales (los que cometen infracciones) y futbolistas legales (los que no las cometen). Obviamente, ningún jugador o nunca infringe las reglas o las infringe al 100% , pero ésto es sólo una simplificación que nos ayudará a entender lo que quiero explicar.
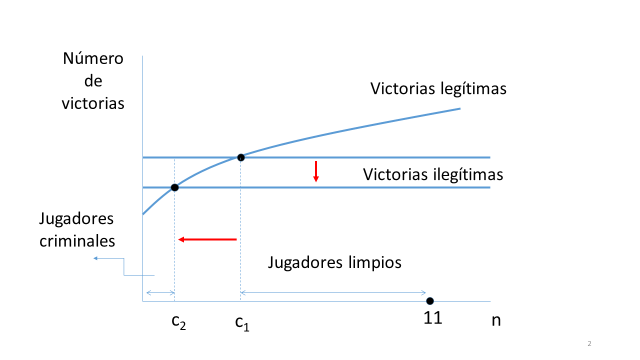
En este modelo los futbolistas criminales son individuos racionales que maximizan su utilidad y que lo único que les importa es el beneficio que obtienen con ello. Supongamos que este beneficio se puede medir con la probabilidad G de ganar el partido. Cuando un jugador comete una infracción, la probabilidad de ser descubierto (y, por lo tanto, sancionado) es p. En caso de ser sancionado, el jugador recibe una penalización (en forma de advertencia, tarjeta, expulsión, etc…) a la que llamamos J. Finalmente, cometer una infracción tiene un coste adicional, e, que incluye el esfuerzo físico necesario (por ejemplo, arriesgarse a una lesión al hacer una entrada dura), así como el coste social de ser considerado un jugador criminal (sería fácil pensar en algunos ejemplos, pero seamos políticamente correctos…). Con todos estos supuestos, el valor esperado de cometer una infracción viene dado por (1-p)G – pJ – e. Supongamos que podemos ordenar a los jugadores por su calidad innata, de forma que los futbolistas más a la derecha del eje de abscisas tienen una mayor capacidad de ganar con sus acciones legales. Messi y Ronaldo, por ejemplo, estarían en el extremo derecho del eje de abscisas. La curva “victorias legítimas” indica que, a mayor calidad del jugador, mayor la probabilidad de que sus acciones lleven a que su equipo gane el partido. Por otro lado, supongamos que, si un futbolista decide hacerse “criminal”, es decir, usar de forma sistemática acciones antirreglamentarias, la probabilidad de ganar partidos es la misma independientemente de qué jugador se trate. Básicamente, estoy asumiendo que, si Messi hace trampas, eso repercute exactamente igual en probabilidad de que el Barca gane un partido que si es Jordi Alba el que hace trampas. Esto viene representado por la línea a la que llamo “victorias ilegítimas”. El siguiente gráfico muestra que, en este modelo, de los 11 jugadores que hay en un equipo, aquellos que estén a la izquierda de c deciden hacerse futbolistas criminales (les sale más a cuenta), y a la derecha de este nivel crítico, se hacen futbolistas legales. El modelo predice, por cierto, que es más probable que los jugadores de menos calidad sean criminales, algo que sería interesante contrastar algún día.
¿Qué tiene que ver el VAR con todo esto? El principal efecto de esta nueva tecnología es que, una vez un jugador comete una acción irregular, la probabilidad de ser cazado, p, es mayor que antes del uso del VAR. Es fácil ver que el modelo predice entonces que el VAR implica un menor número de infracciones en el juego. El motivo es que un mayor valor de p mueve la curva de victorias criminales abajo (el valor esperado de cometer un crimen es menor) y hace que algunos jugadores decidan dejar de cometer infracciones anticipando que es más probable que sean castigados. Nótese que el castigo en caso de ser pillado, J, no ha cambiado. Por ejemplo, un nuevo reglamento que penalizara más las entradas feas, se correspondería a un aumento en este parámetro. El efecto del VAR en el número de infracciones se muestra en el siguiente gráfico:
El modelo de Becker es pues muy claro en cuanto a su predicción sobre el efecto del VAR. ¿Apoyan los datos esta predicción? Pues la verdad es que aún es un poco pronto para decirlo. Sin embargo, El País apuntaba hace unas semanas que ésto es precisamente lo que estamos viendo en las pocas jornadas que llevamos de liga (ver aquí): la implantación del VAR parece coincidir con el menor número de faltas y tarjetas de los últimos 11 años. Obviamente, para hacer ésto bien, habría que esperar al final de temporada y además habría que llevar a cabo un análisis de datos serio para asegurarse que nada más ha cambiado este año en la liga española que justifique un cambio pronunciado en el número de infracciones. Por ejemplo, este libro de Natxo Palacios-Huerta (ver aquí) habla en detalle de muchos factores que pueden afectar el comportamiento de los jugadores.
La verdad es que un servidor aún no ha tenido tiempo de mirarlo en detalle, pero junto a mi estudiante Shabani Kariburyo hemos recogido datos de los últimos 6 mundiales y parecen ser consistentes con la predicción del modelo: el número de tarjetas rojas (4) del último mundial fue muchísimo menor que la media de tarjetas rojas en los anteriores cinco Mundiales (18). También se observa un significativo, aunque menor, descenso en el número de tarjetas amarillas (219 vs. 255). Por otro lado, el número de goles ha aumentado ligeramente (169 vs 159) tal vez – aunque esto es mucho más especulativo- también debido a la introducción del VAR: es posible que la reducción del crimen en el terreno de juego permita a los jugadores marcar más goles.
Por cierto, no sería la primera vez que el modelo de Becker se usa para este tipo de análisis. Hace ya años, el prolífico economista Bob Tollison del que hable aquí hace algún tiempo y su coautor Bobby McCormick mostraron, en un excelente articulo (ver aquí), cómo la introducción de un tercer arbitro (antes solo había dos) en el baloncesto universitario de Estados Unidos redujo de forma muy marcada el número de faltas cometidas en los partidos.