de Jordi Massó
Lloyd S. Shapley falleció el sábado 12 de marzo de 2016 a la edad de 92 años en Tucson, Arizona. Su salud, ya precaria, empeoró hace pocas semanas al romperse la cadera. Shapley es uno de los precursores (y contribuidores) más importantes de la teoría de los juegos.
Shapley nace en Cambridge (Nueva Inglaterra) el 2 de junio de 1923. Después de servir en el cuerpo aéreo del ejército de los Estados Unidos en Chengdu, China, durante la Segunda Guerra Mundial, vuelve a la universidad de Harvard en donde reemprende sus estudios de matemáticas y se gradúa el año 1948. Obtiene el doctorado en matemáticas en la universidad de Princeton en 1953 bajo la supervisión de Albert W. Tucker (quién también supervisó la tesis de John F. Nash, defendida en 1950). Su tesis doctoral trataba sobre las funciones multivalor aditivas y no aditivas. Shapley sólo ha tenido dos afiliaciones: la RAND Corporation, entre 1954 y 1981, y los departamentos de matemáticas y economía en la universidad de California en Los Ángeles, desde 1981 hasta la actualidad (a partir de 2001 como profesor emérito).
Shapley recibe el premio Sveriges Riskbank en ciencias económicas en memoria de Alfred Nobel en 2012 junto con Alvin E. Roth (profesor de economía en la universidad de Stanford) por “sus contribuciones a la teoría de las asignaciones estables y a la práctica del diseño de mercados”. La teoría de las asignaciones estables consiste en una familia de modelos que estudian problemas de asignación en los que dos conjuntos disjuntos de agentes (o un conjunto de agentes y un conjunto de objetos) tienen que asignarse bilateralmente, teniendo en cuenta las preferencias que cada agente tiene sobre los agentes del otro conjunto. Por ejemplo, hombres a mujeres, trabajadores a empresas, estudiantes a escuelas públicas, médicos internos residentes a programas hospitalarios o riñones de donantes a pacientes renales. Una asignación bilateral es un conjunto de parejas formadas por agentes de distintos conjuntos, y es estable si no existe ningún par de agentes que no están asignados entre ellos, pero preferirían estarlo. La estabilidad de la asignación bilateral es indispensable si los agentes participan voluntariamente en la institución que propone la asignación bilateral. La práctica del diseño de mercados consiste en aplicar estos modelos de asignación bilateral (y otros métodos como la computación y los experimentos) a problemas específicos de asignación bilateral en mercados cuando, por razones éticas o legales, no pueden usarse los precios para equilibrar los excesos de demanda o de oferta. El objetivo del diseño de mercados consiste en proponer modificaciones en los mecanismos y procedimientos utilizados para mejorar la asignación bilateral entre los agentes en los dos lados del mercado. La concesión del premio Nobel de economía, conjuntamente con Roth, puede ser entendida como el reconocimiento a dos partes complementarias de una misma investigación: a Shapley por las aportaciones teóricas a la teoría de las asignaciones bilaterales estables (ver referencias [1] y [2]) y a Roth por las aplicaciones de esta teoría a problemas reales de asignación bilateral en mercados con el fin de mejorar su funcionamiento. David Gale, estudiante como Nash y Shapley de Albert W. Tucker en Princeton, y que falleció en 2008, también hizo aportaciones cruciales a la teoría de las asignaciones bilaterales estables, por lo que es razonable pensar que de estar vivo en 2012 hubiera podido recibir el premio junto con Roth y Shapley.
Pero Shapley ha hecho contribuciones fundamentales en todas las áreas de la teoría de los juegos. Por ejemplo, participó en los primeros estudios del núcleo, propuso el valor de Shapley como la solución a los juegos cooperativos con utilidad transferible, inició el análisis de los juegos repetidos y estocásticos, formuló la noción del potencial de un juego y contribuyó a la ya mencionada teoría de las asignaciones bilaterales estables, entre muchas otras. Muchos pensábamos, antes del mes de octubre de 2012, que el hecho de que Shapley no hubiera recibido aún el premio Nobel de economía era una triste omisión, y nos alegramos cuando lo recibió.
Entre todas sus contribuciones, una de la más importante es la del valor de Shapley (ver referencia [3]), y es la que desarrollaré en lo que resta de entrada. El valor de Shapley es un concepto de solución para los juegos cooperativos con utilidad transferible. Un juego cooperativo con utilidad transferible consiste en dos objetos: (a) el conjunto N={1,…,n} de jugadores y (b) para cada coalición S (subconjunto de N) una descripción, resumida en un número v(S) que representa la utilidad (o dinero para simplificar), de lo que la coalición S puede asegurarse coordinando las acciones de sus miembros, independientemente del comportamiento de los jugadores que no pertenecen a la coalición. A la familia de todos estos números, uno por coalición, se le llama la función característica v (o directamente juego) y es como un resumen de las consecuencias de la interacción estratégica entre los jugadores que obvia los detalles potencialmente complejos de cómo ésta se realiza (que es el punto de vista adoptado por los juegos no cooperativos). Una solución f es un criterio que, para cada juego cooperativo con utilidad transferible v, asigna a cada jugador i un único número que indica el valor que tiene para i jugar el juego v, representado por f[i](v). Una solución es por lo tanto una función que asigna a cada juego v un vector f(v)=(f[1](v),…,f[n](v)), cuyos componentes pueden ser interpretados como las expectativas de los jugadores derivadas de participar en el juego. Y éstas, claro, deberían depender de la contribución que el jugador hace a la utilidad total de cada una de las coaliciones a las que él puede pertenecer. La aproximación utilizada por Shapley para hallar una solución es axiomática. Dado cualquier juego v, se pregunta: ¿qué debería recibir cada jugador en v? Para dar respuesta a esta pregunta propone un conjunto de propiedades deseables que cualquier solución debería cumplir, y luego demuestra que existe una única solución que las satisface todas simultáneamente: el valor de Shapley. La primera propiedad es la de eficiencia: la solución debería repartir v(N), la cantidad máxima que se puede obtener en el juego (se supone que v es superaditivo). La segunda es la de simetría: si dos jugadores aportan lo mismo al unirse a todas y cada una de las coaliciones a las que no pertenecen, deberían recibir lo mismo. La tercera propiedad es la de jugador nulo: si un jugador no contribuye a ninguna coalición, debería recibir cero (lo que v asigna al conjunto vacío de jugadores). Y finalmente la cuarta propiedad, la de naturaleza más técnica, es la de linealidad, cuya interpretación más sencilla es la siguiente. Si un jugador i se enfrenta a la posibilidad de que se juegue v con probabilidad p o se juegue u con probabilidad 1-p, entonces la solución del juego ponderado p·v+(1-p)·u para i (es decir, f[i](p·v+(1-p)·u)) es igual a p.f[i](v)+(1-p)·f[i](v)), la solución esperada de que se juegue cada uno de los juegos, con sus respectivas probabilidades. El teorema de Shapley dice que existe una única solución que satisface eficiencia, simetría, jugador nulo y linealidad, y ésta es el valor de Shapley, la solución Sh, cuya forma funcional es muy sencilla. Para cada v y cada i,
donde s es la cardinalidad del conjunto S, que tiene la siguiente interpretación. Supongamos que ordenamos a los jugadores de manera aleatoria (la probabilidad de que cada uno de los órdenes ocurra es igual a 1/n!, ya que n! es el número de maneras distintas de ordenar el conjunto N). Consideremos un orden determinado, y supongamos que, siguiendo este orden, los jugadores van entrando en una sala. Para cada jugador i calculamos su contribución marginal a la coalición S formada por los jugadores que están en la sala, justo en el momento en que i entra en ella; es decir, v(S{i})-v(S) es la contribución marginal de i a la coalición S y ![]() es la probabilidad de que cuando i entra en la sala haya exactamente el conjunto S en la misma. El valor de Shapley para el jugador i en el juego v, Sh[i](v), es entonces el valor esperado de las contribuciones marginales de i cuando todos los órdenes son equiprobables.
es la probabilidad de que cuando i entra en la sala haya exactamente el conjunto S en la misma. El valor de Shapley para el jugador i en el juego v, Sh[i](v), es entonces el valor esperado de las contribuciones marginales de i cuando todos los órdenes son equiprobables.
En la cena de gala de la entrega de los premios Nobel del 2012, Roth empieza su discurso, refiriéndose a la célebre metáfora popularizada por Isaac Newton, diciendo que los científicos somos como enanos que podemos otear el horizonte lejano porque estamos subidos sobre hombros de gigantes. Shapley era sin duda uno de estos gigantes, y de los más grandes: un gigante entre gigantes.
Referencias básicas
[1] David Gale y Lloyd S. Shapley. “College admissions and the stability of marriage”, American Mathematical Monthly 69, 9-15 (1962).
[2] Lloyd S. Shapley y Herbert E. Scarf. “On cores and indivisibilities”, Journal of Mathematical Economics 1, 23-28 (1974).
[3] Lloyd S. Shapley. “A value for n-person games”, en Contributions to the Theory of Games II. Editores: Harold W. Kuhn y Albert W. Tucker. Princeton University Press (1953).


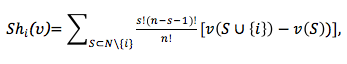

Hay 1 comentarios
Gracias Jordi por este homenaje a Shapley.
Él mismo se extrañó de la concesión del Nobel en Economía a un matemático por un paper que le habían rechazado dos veces por ser muy simple... Seguro que esta anécdota pone de manifiesto su humildad.
Es difícil glosar las múltiples e importantes aportaciones de las que hemos disfrutado los economistas, como el elegante modelado de los "housing markets" o su función de valor para juegos no-atómicos (con Aumann) y su aplicación a pricing models...
Ciertamente una gran pérdida.
Los comentarios están cerrados.